
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

【答案】证明见解析
【解析】试题分析:(1)根据已知求得∠BDF=∠BCD,再根据∠BFD=∠DFC,证明△BFD∽△DFC,从而得BF:DF=DF:FC,进行变形即得;
(2)由已知证明△AEG∽△ADC,得到∠AEG=∠ADC=90°,从而得EG∥BC,继而得![]() ,
,
由(1)可得![]() ,从而得
,从而得![]() ,问题得证.
,问题得证.
试题解析:(1)∵∠ACB=90°,∴∠BCD+∠ACD=90°,
∵CD是Rt△ABC的高,∴∠ADC=∠BDC=90°,∴∠A+∠ACD=90°,∴∠A=∠BCD,
∵E是AC的中点,
∴DE=AE=CE,∴∠A=∠EDA,∠ACD=∠EDC,
∵∠EDC+∠BDF=180°-∠BDC=90°,∴∠BDF=∠BCD,
又∵∠BFD=∠DFC,
∴△BFD∽△DFC,
∴BF:DF=DF:FC,
∴DF2=BF·CF;
(2)∵AE·AC=ED·DF,
∴![]() ,
,
又∵∠A=∠A,
∴△AEG∽△ADC,
∴∠AEG=∠ADC=90°,
∴EG∥BC,
∴![]() ,
,
由(1)知△DFD∽△DFC,
∴![]() ,
,
∴![]() ,
,
∴EG·CF=ED·DF.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作已知角的角平分线.
已知:如图,已知![]() .
.
求作: ![]() 的角平分线
的角平分线![]() .
.

小霞的作法如下:
(1)如图,在平面内任取一点![]() ;
;
(2)以点![]() 为圆心,
为圆心, ![]() 为半径作圆,交射线
为半径作圆,交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ;
;
(3)连接![]() ,过点
,过点![]() 作射线
作射线![]() 垂直线段
垂直线段![]() ,交⊙
,交⊙![]() 于点
于点![]() ;
;
(4)连接![]() .
.

所以射线![]() 为所求.
为所求.
老师说:“小霞的作法正确.”
请回答:小霞的作图依据是___________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
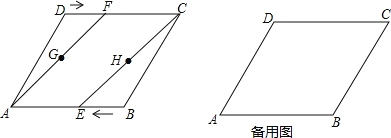
【题目】如图,在菱形![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,以
同时出发,以![]() 的速度向点
的速度向点![]() 、
、![]() 运动,连接
运动,连接![]() 、
、![]() ,取
,取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() .设运动的时间为
.设运动的时间为![]() .
.
(1)求证:![]() ;
;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 为菱形;
为菱形;
(3)试探究:是否存在某个时刻![]() ,使四边形
,使四边形![]() 为矩形,若存在,求出
为矩形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】许多代数恒等式可以借助图形的面积关系直观表达,如图①,根据图中面积关系可以得到:![]() 。
。

(1)如图②,根据图中面积关系,写出一个关于![]() 的等式 ;
的等式 ;
(2)利用(1)中的等式求解:![]() ,则
,则![]() ;
;
(3)小明用8个面积一样大的长方形(宽![]() ,长
,长![]() )拼图,拼出了如图甲、乙的两种图案;图案甲是一个大的正方形,中间阴影部分是边长为3的小正方形;图案乙是一个大的长方形,求
)拼图,拼出了如图甲、乙的两种图案;图案甲是一个大的正方形,中间阴影部分是边长为3的小正方形;图案乙是一个大的长方形,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
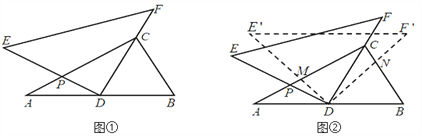
【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角![]() ,此时等腰直角三角尺记为
,此时等腰直角三角尺记为![]() ,
, ![]() 交AC于点M,
交AC于点M, ![]() 交BC于点N,试判断
交BC于点N,试判断![]() 的值是否随着
的值是否随着![]() 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出![]() 的值;反之,请说明理由.
的值;反之,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点A﹙2,4﹚、C﹙4,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙2,4﹚、C﹙4,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)连接OA、OC,求△AOC的面积;
(3)写出使一次函数的值大于反比例函数的![]() 的取值范围 .
的取值范围 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形![]() 折叠,使
折叠,使![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() ;
;
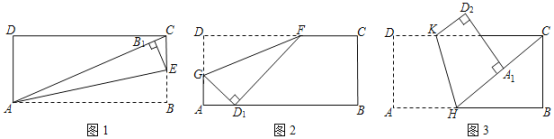
(2)小丽手中有一张矩形纸片,![]() ,
,![]() .她准备按如下两种方式进行折叠:
.她准备按如下两种方式进行折叠:
①如图2,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使点
上,将纸片折叠,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
②如图3,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 处,若
处,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83 乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 ,乙成绩的平均数是 ;
(2)求甲、乙两名同学测试成绩的方差S甲2与S乙2.
(3)请你选择一个角度来判断选拔谁参加比赛更合适.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
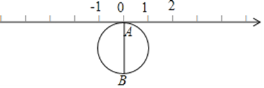
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com