Question

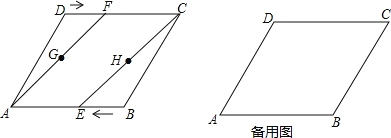
【题目】如图，在菱形，，.动点、分别从点、同时出发，以的速度向点、运动，连接、，取、的中点、，连接、.设运动的时间为.

（1）求证：；

（2）当为何值时，四边形为菱形；

（3）试探究：是否存在某个时刻，使四边形为矩形，若存在，求出的值，若不存在，请说明理由.

Answer 1

【答案】（1）证明详见解析；（2）1；（3）不存在，理由详见解析

【解析】

（1）根据菱形的性质得到∠B=∠D，AD=BC，AB∥DC，推出△ADF≌△CBE，根据全等三角形的性质得到∠DFA=∠BEC，根据平行线的判定定理即可得到结论；

（2）过D作DM⊥AB于M，连接GH，EF，推出四边形AECF是平行四边形，根据菱形的判定定理即可得到四边形EGFH是菱形，证得四边形DMEF是矩形，于是得到ME=DF=t列方程即可得到结论；

（3）不存在，假设存在某个时刻t，使四边形EHFG为矩形，根据矩形的性质列方程即可得到结果．

解：（1）证明：∵动点E、F同时运动且速度相等，

∴DF=BE，

∵四边形ABCD是菱形，

∴∠B=∠D，AD=BC，AB∥DC，

在△ADF与△CBE中，

，

∴△ADF≌△CBE，

∴∠DFA=∠BEC，

∵AB∥DC，

∴∠DFA=∠FAB，

∴∠FAB=∠BEC，

∴AF∥CE；

（2）如图，过D作DM⊥AB于M，连接GH，EF，

∴DF=BE=t，

∵AF∥CE，AB∥CD，

∴四边形AECF是平行四边形，

∵G、H是AF、CE的中点，

∴GH∥AB，

∵四边形EGFH是菱形，

∴GH⊥EF，

∴EF⊥AB，∠FEM=90°，

∵DM⊥AB，

∴DM∥EF，

∴四边形DMEF是矩形，

∴ME=DF=t，

∵AD=4，∠DAB=60°，DM⊥AB，

∴，

∴BE=4-2-t=t，

∴t=1；

（3）不存在，假设存在某个时刻t，使四边形EHFG为矩形，

∵四边形EHFG为矩形，

∴EF=GH，

∴，

即，

解得t=0，0＜t＜4，

∴与原题设矛盾，

∴不存在某个时刻t，使四边形EHFG为矩形．