
【题目】如图, ![]() 是⊙O的直径,点
是⊙O的直径,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,
, ![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,
, ![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 是⊙O的切线;
是⊙O的切线;
(2)当![]() 时,求
时,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)BH =![]() .
.
【解析】试题分析:(1)连接OC,由题意可得∠AOC=90°,OC//BD,从而得OB与BD垂直,问题得证;
(2)先证明△OCE∽△BFE,根据相似三角形对应边成比例以及![]() ,求得BF=3,在Rt
,求得BF=3,在Rt![]() 中,利用勾股定理求得
中,利用勾股定理求得![]() ,再利用
,再利用![]() 即可得.
即可得.
试题解析:(1)连接OC,

∵AB为⊙O的直径,点![]() 是
是![]() 的中点,∴∠AOC=90°,
的中点,∴∠AOC=90°,
∵![]() ,∴OC是
,∴OC是![]() 的中位线,∴OC∥BD,
的中位线,∴OC∥BD,
∴∠ABD=∠AOC=90°,
∴![]() ,
,
∴![]() 是⊙O的切线;
是⊙O的切线;
(2)由(1)知OC∥BD,∴△OCE∽△BFE,∴ ![]() ,
,
∵OB = 2,∴OC= OB = 2,AB = 4,∵ ![]() ,∴
,∴![]() ,∴BF=3,
,∴BF=3,
在Rt![]() 中,∠ABF=90°,
中,∠ABF=90°,![]() ,
,
∵![]() ,
,
∴![]() .即
.即![]() ,
,
∴BH =![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3),B点坐标为(﹣2,0),C点坐标为(0,﹣1).
(1)S△ABC= ;
(2)若以A、B、C及点D为顶点的四边形为平行四边形,试在图中画出所有D点的位置并求出这些平行四边形中最长的对角线长为 ,最短的对角线长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于M,DN⊥AC的延长线于N.
(1)求证:BM=CN;
(2)若AB=8,AC=4,求BM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y = x2 - 4x + 3.
(1)用配方法将y = x2 - 4x + 3化成y = a(x - h)2 + k的形式;
(2)在平面直角坐标系![]() 中画出该函数的图象;
中画出该函数的图象;
(3)当0≤x≤3时,y的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求不等式(2x﹣1)(x+3)>0的解集.
解:根据“同号两数相乘,积为正”可得:①![]() 或 ②
或 ②![]() .
.
解①得x>![]() ;解②得x<﹣3.
;解②得x<﹣3.
∴不等式的解集为x>![]() 或x<﹣3.
或x<﹣3.
请你仿照上述方法解决下列问题:
(1)求不等式(2x﹣3)(x+1)<0的解集.
(2)求不等式![]() ≥0的解集.
≥0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为______元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作已知角的角平分线.
已知:如图,已知![]() .
.
求作: ![]() 的角平分线
的角平分线![]() .
.

小霞的作法如下:
(1)如图,在平面内任取一点![]() ;
;
(2)以点![]() 为圆心,
为圆心, ![]() 为半径作圆,交射线
为半径作圆,交射线![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() ;
;
(3)连接![]() ,过点
,过点![]() 作射线
作射线![]() 垂直线段
垂直线段![]() ,交⊙
,交⊙![]() 于点
于点![]() ;
;
(4)连接![]() .
.

所以射线![]() 为所求.
为所求.
老师说:“小霞的作法正确.”
请回答:小霞的作图依据是___________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
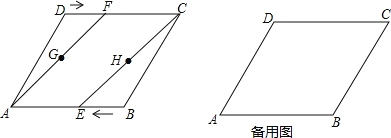
【题目】如图,在菱形![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,以
同时出发,以![]() 的速度向点
的速度向点![]() 、
、![]() 运动,连接
运动,连接![]() 、
、![]() ,取
,取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() .设运动的时间为
.设运动的时间为![]() .
.
(1)求证:![]() ;
;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 为菱形;
为菱形;
(3)试探究:是否存在某个时刻![]() ,使四边形
,使四边形![]() 为矩形,若存在,求出
为矩形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com