
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
【答案】(1)打折前甲品牌粽子每盒70元,乙品牌粽子每盒80元.(2)打折后购买这批粽子比不打折节省了3120元.
【解析】
(1)设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元,根据“打折前,买6盒甲品牌粽子和3盒乙品牌粽子需600元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据节省钱数=原价购买所需钱数-打折后购买所需钱数,即可求出节省的钱数.
(1)设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元,
根据题意得:
![]() ,
,
解得:![]() .
.
答:打折前甲品牌粽子每盒40元,乙品牌粽子每盒120元.
(2)80×40+100×120-80×0.8×40-100×0.75×120=3640(元).
答:打折后购买这批粽子比不打折节省了3640元.


科目:初中数学 来源: 题型:
【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )

A. ①② B. ①③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明和小颖相约到乐山大佛景区参观.小明乘私家车从成都出发1小时后,小颖乘坐高铁从成都出发,先到乐山高铁站,然后转乘出租车到乐山大佛景区(换车时间忽略不计),两人恰好同时到达景区.他们离开成都的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.
(1)高铁的平均速度是每小时多少千米?
(2)当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= ![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为(、),BK的长是 , CK的长是;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2 , 在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校要建一个面积是81平方米的草坪,草坪周围用铁栅栏围绕,现有两种方案:有人建议建成正方形,也有人建议建成圆形,如果从节省铁栅栏费用的角度考虑(栅栏周长越小,费用越少),你选择哪种方案?请说明理由.(π取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的图形均可以由“基本图案”通过变换得到.(填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是__;
(2)可以通过旋转变换但不能通过平移变换得到的图案是__;
(3)既可以由平移变换,也可以由旋转变换得到的图案是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
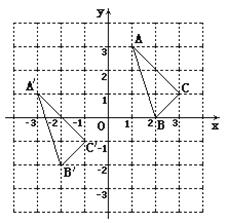
【题目】△ A B C与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标: ![]() ______ ;
______ ; ![]() _______ ;
_______ ; ![]() _______ ;
_______ ;
(2)说明![]() 由△ A B C经过怎样的平移得到? ________________________________.
由△ A B C经过怎样的平移得到? ________________________________.
(3)若点![]() (
(![]() ,
, ![]() )是△ A B C内部一点,则平移后
)是△ A B C内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为 ________ ;
的坐标为 ________ ;
(4)求△ A B C的面积..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。

(1)求证:四边形CMAN是平行四边形。
(2)已知DE=4,FN=3,求BN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2 , …,Bn , 以线段AnBn为边向左作正方形AnBnCnDn , 如果这组抛物线中的某一条经过点Dn , 求此时满足条件的正方形AnBnCnDn的边长.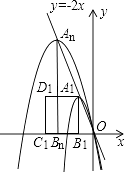
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com