
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= ![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为(、),BK的长是 , CK的长是;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2 , 在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
【答案】
(1)10,0,8,10
(2)解:不变.S1S2=289.
理由:如图2中,
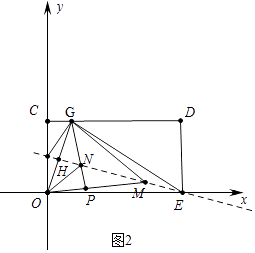
在Rt△EDG中,∵GE=EO=17,ED=8,
∴DG= ![]() =
= ![]() =15,
=15,
∴CG=CD﹣DG=2,
∴OG= ![]() =
= ![]() =2
=2 ![]() ,
,
∵GP⊥OM,MH⊥OG,
∴∠NPN=∠NHG=90°,
∵∠HNG+∠HGN=90°,∠PNM+∠PMN=90°,∠HNG=∠PNM,
∴∠HGN=∠NMP,
∵∠NMP=∠HMG,∠GHN=∠GHM,
∴△GHN∽△MHG,
∴ ![]() =
= ![]() ,
,
∴GH2=HNHM,
∵GH=OH= ![]() ,
,
∴HNHM=17,
∵S1S2= ![]() OGHN
OGHN ![]() OGHM=(
OGHM=( ![]() ×2
×2 ![]() )217=289
)217=289
【解析】S1S2解:(1)如图1中,
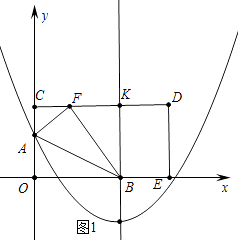
①∵抛物线y= ![]() x2﹣3x+m的对称轴x=﹣
x2﹣3x+m的对称轴x=﹣ ![]() =10,
=10,
∴点B坐标(10,0),
∵四边形OBKC是矩形,
∴CK=OB=10,KB=OC=8,
故答案分别为10,0,8,10.
②在Rt△FBK中,∵∠FKB=90°,BF=OB=10,BK=OC=8,
∴FK= ![]() =6,
=6,
∴CF=CK﹣FK=4,
∴点F坐标(4,8).
③设OA=AF=x,
在Rt△ACF中,∵AC2+CF2=AF2,
∴(8﹣x)2+42=x2,
∴x=5,
∴点A坐标(0,5),
代入抛物线y= ![]() x2﹣3x+m得m=5,
x2﹣3x+m得m=5,
∴抛物线为y= ![]() x2﹣3x+5.
x2﹣3x+5.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.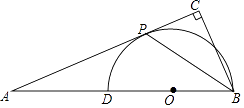
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )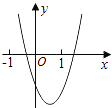
A.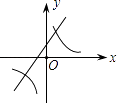
B.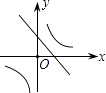
C.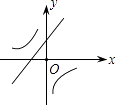
D.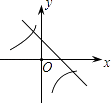
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?
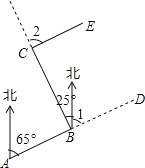
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )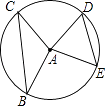
A.8
B.10
C.11
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE
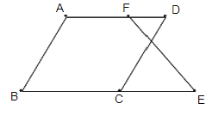
证明:∵∠B+∠BCD=180°(已知)
∴AB∥CD( )
∴∠B=∠DCE( )
又∵∠B=∠D(已知 ),
∴___________ (等量代换)
∴ ∥
∴∠E=∠DFE( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com