
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )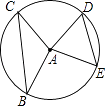
A.8
B.10
C.11
D.12
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】下面是两位同学的一段对话:
聪聪:周末我们去国家博物馆参观“伟大的变革﹣﹣庆祝改革开放40周年大型展览”吧.
明明:好啊,我家离国家博物馆约30km,我坐地铁先走,地铁的平均行驶速度是公交车的1.5倍呢.
聪聪:嗯,我周末住奶奶家,离国家博物馆只有5km,坐公交车,你出发40分钟后我再出发就能和你同时到达.
根据对话内容,请你求出公交车和地铁的平均行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
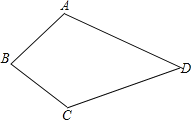
【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= ![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为(、),BK的长是 , CK的长是;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2 , 在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的图形均可以由“基本图案”通过变换得到.(填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是__;
(2)可以通过旋转变换但不能通过平移变换得到的图案是__;
(3)既可以由平移变换,也可以由旋转变换得到的图案是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2﹣4ac>0;④﹣ ![]() <0,正确的是( )
<0,正确的是( )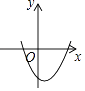
A.①②
B.②④
C.①③
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com