
【题目】如图,锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D.请写出图中的一对相似三角形,如 . 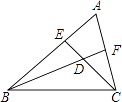
【答案】△ABF∽△DBE或△ACE∽△DCF或△EDB∽△FDC
【解析】解:∵锐角三角形ABC的边AB和AC上的高线CE和BF相交于点D
∴∠AEC=∠BEC=∠AFB=∠CFB=90°
∵∠ABF=∠DBE,∠ACE=∠DCF
∴△ABF∽△DBE,△ACE∽△DCF
∵∠EDB=∠FDC
∴△EDB∽△FDC
∴△ABF∽△DBE∽△DCF∽△ACE
答案不唯一,如△ABF∽△DBE或△ACE∽△DCF或△EDB∽△FDC等.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD= . 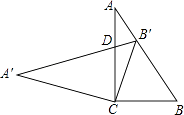
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧 ![]() 上的一点,则cos∠APB的值是( )
上的一点,则cos∠APB的值是( )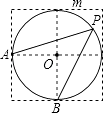
A.45°
B.1
C.![]()
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )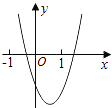
A.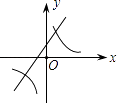
B.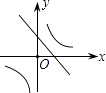
C.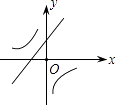
D.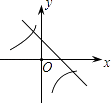
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为_____.
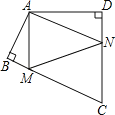
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )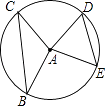
A.8
B.10
C.11
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com