
【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=ax2﹣b的图象可能是( )
A.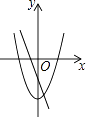
B.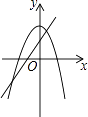
C.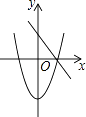
D.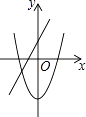
【答案】D
【解析】A、由直线y=ax+b的图象经过第二、三、四象限可知:a<0,b<0,
二次函数y=ax2﹣b的图象开口向上,∴a>0,A不正确,A不符合题意;
B、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向下,∴a<0,B不正确,B不符合题意;
C、由直线y=ax+b的图象经过第一、二、四象限可知:a<0,b>0,
二次函数y=ax2﹣b的图象开口向上,∴a>0,C不符合题意;
D、由直线y=ax+b的图象经过第一、二、三象限可知:a>0,b>0,
二次函数y=ax2﹣b的图象开口向上,顶点在y轴负半轴,
∴a>0,b>0,D符合题意.
所以答案是:D.
【考点精析】掌握一次函数的图象和性质和二次函数的图象是解答本题的根本,需要知道一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


科目:初中数学 来源: 题型:
【题目】图中的图形均可以由“基本图案”通过变换得到.(填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是__;
(2)可以通过旋转变换但不能通过平移变换得到的图案是__;
(3)既可以由平移变换,也可以由旋转变换得到的图案是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。

(1)求证:四边形CMAN是平行四边形。
(2)已知DE=4,FN=3,求BN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
| 30 | 0.1 |
| 90 |
|
|
| 0.4 |
| 60 | 0.2 |
(Ⅰ)本次调查的样本容量为______;
(Ⅱ)在表中,![]() ______,
______,![]() ______;
______;
(Ⅲ)补全频数分布直方图;

(Ⅳ)如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )
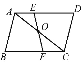
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2﹣4ac>0;④﹣ ![]() <0,正确的是( )
<0,正确的是( )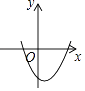
A.①②
B.②④
C.①③
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:
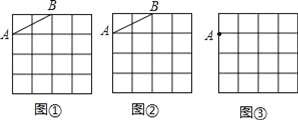
(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;
(2)在图②中,以格点为顶点,AB为一边画一个正方形;
(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com