
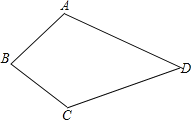
【题目】(A类)已知如图,四边形ABCD中,AB=BC,AD=CD,求证:∠A=∠C.
(B类)已知如图,四边形ABCD中,AB=BC,∠A=∠C,求证:AD=CD.
【答案】(A类)证明见解析;(B类)证明见解析.
【解析】
(A类)连接AC,由AB=AC、AD=CD知∠BAC=∠BCA、∠DAC=∠DCA,两等式相加即可得;
(B类)连接AC,由AB=BC,可得∠BAC=∠BCA,再根据∠BAD=∠BCD则可得∠DAC=∠DCA,根据等腰三角形的判定即可得AD=CD.
(A类)连接AC,
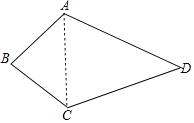
∵AB=AC,AD=CD,
∴∠BAC=∠BCA,∠DAC=∠DCA,
∴∠BAC+∠DAC=∠BCA+∠DCA,
即∠BAD=∠BCD;
(B类)连接AC,
∵AB=BC,
∴∠BAC=∠BCA,
又∵∠BAD=∠BCD,即∠BAC+∠DAC=∠BCA+∠DCA,
∴∠DAC=∠DCA,
∴AD=CD.


科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中记载了一个“折竹抵地”问题:“今有竹高二丈,末折抵地,去本六尺,问折者高几何?”
译文:“有一根竹子,原高二丈(1丈=10尺),现被风折断,竹梢触地面处与竹根的距离为6尺,问折断处离地面的高度为多少尺?”
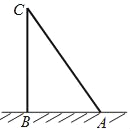
如图,我们用点A,B,C分别表示竹梢,竹根和折断处,设折断处离地面的高度BC=x尺,则可列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧 ![]() 上的一点,则cos∠APB的值是( )
上的一点,则cos∠APB的值是( )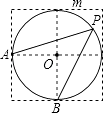
A.45°
B.1
C.![]()
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
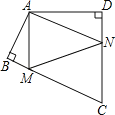
【题目】四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱动脑筋的小明同学在买一双新的运动鞋时,发现了一个有趣现象:即鞋子的码数y(码)与鞋子的长x(cm)之间存在着某种联系.经过收集数据,得到如表:
鞋长x(cm) | … | 22 | 23 | 24 | 25 | 26 | … |
码数y(码) | … | 34 | 36 | 38 | 40 | 42 | … |
请你替小明解决下列问题:
(1)当鞋长为28cm时,鞋子的码数是多少?
(2)写出y与x之间的关系式;
(3)已知姚明的鞋子穿52码时,则他穿的鞋长是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )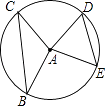
A.8
B.10
C.11
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划用![]() 元从厂家购进
元从厂家购进![]() 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入![]() 台,其中每台的价格、销售获利如下表:
台,其中每台的价格、销售获利如下表:
甲型 | 乙型 | 丙型 | |
价格(元/台) |
|
|
|
销售获利(元/台) |
|
|
|
![]() 购买丙型设备 台(用含
购买丙型设备 台(用含![]() 的代数式表示) ;
的代数式表示) ;
![]() 若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了![]() 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?
![]() 在第
在第![]() 题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com