【题目】如图，PA、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，交PA、PB于点E、F，已知PA=12cm，∠P=40°
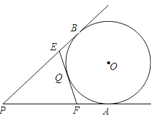
（1）求△PEF的周长.
（2）求∠EOF的度数.
【答案】（1）24cm；（2）70°.
【解析】
①根据切线长定理得出PA=PB，EB=EQ，FQ=FA，由PE+EF+PF=PE+EQ+FQ+PF即可求出答案．
②连接OE，OF，求出∠OEF+∠OFE的度数，即可得出∠EOF的度数．
（1）解：∵PA、PB是⊙O的切线，
∴PA=PB，
又∵直线EF是⊙O的切线，
∴EB=EQ，FQ=FA，
∴△PEF的周长=PE+PF+EF=PE+PF+EB+FA=PA+PB=2PA=24cm
（2）解：
连接OE，OF，则OE平分∠BEF，OF平分∠AFE，
则∠OEF+∠OFE=
（∠P+∠PFE）+∠（P+∠PEF）=（180°+40°）=110°，
∴∠EOF=180°﹣110°=70°．
科目：初中数学 来源： 题型：
【题目】如图，为测量某建筑物AB的高度，在离该建筑物底部20m的点C处，目测建筑物顶端A处，视线与水平线夹角∠ADE为38.5°，目高CD为1.6m．求建筑物AB的高度．（结果精确到1m）（参考数据：sin38.5°=0.623，cos38.5°=0.783，tan38.5°=0.795）
查看答案和解析>>
科目：初中数学 来源： 题型：
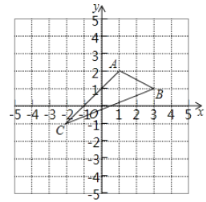
【题目】如图，在平面直角坐标系xoy中，A（1，2），B（3，1），C（﹣2，﹣1）．
（1）在图中作出△ABC关于y轴的对称图形△A1B1C1．
（2）写出点A1，B1，C1的坐标（直接写答案）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个无人超市仓库的货物搬运工作全部由机器人
和机器人
完成，工作记录显示机器人比机器人每小时多搬运50件货物．机器人搬运2000件货物与机器人搬运1600件货物所用的时间相等，则机器人每小时搬运货物（ ）
A.250件B.200件C.150件D.100件
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店计划购进甲、乙两种商品，乙种商品的进价是甲种商品进价的九折，用3600元购买乙种商品要比购买甲种商品多买10件．
（1）求甲、乙两种商品的进价各是多少元？
（2）该商店计划购进甲、乙两种商品共80件，且乙种商品的数量不低于甲种商品数量的3倍．甲种商品的售价定为每件80元，乙种商品的售价定为每件70元，若甲、乙两种商品都能卖完，求该商店能获得的最大利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解，解决问题：
网约车、滴滴打车、共享汽车等新的出行方式越来越受大众欢迎．如图1，是某种网约车的计价规则，车辆行驶
，平均速度为
，则打车费用为
元（不足
元按 元计价）．某日，小明出行时叫了一辆网约车，按上述计价规则，打车费用
（元）与行驶里程
的函数关系如图 2 所示．
（1）当
时，求与
的函数表达式；
（2）若
，求该车行驶的平均速度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度
（单位：
）与足球被踢出后经过的时间
（单位：
）之间的关系如下表：
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论：①足球距离地面的最大高度为
；②足球飞行路线的对称轴是直线
；③足球被踢出
时落地；④足球被踢出
时，距离地面的高度是
.
其中正确结论的个数是（ ）
A．1 B．2 C．3 D．4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，△ABC是等边三角形，点D是AC边上动点，∠CBD＝α，把△ABD沿BD对折，A对应点为A'．
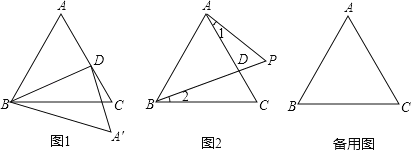
（1）①当α＝15°时，∠CBA'＝ ；
②用α表示∠CBA'为 ．
（2）如图2，点P在BD延长线上，且∠1＝∠2＝α．
①当0°＜α＜60°时，试探究AP，BP，CP之间是否存在一定数量关系，猜想并说明理由．
②BP＝8，CP＝n，则CA'＝ ．（用含n的式子表示）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
