
����Ŀ����ͼ1����ABC�ǵȱ������Σ���D��AC���϶��㣬��CBD����������ABD��BD���ۣ�A��Ӧ��ΪA'��
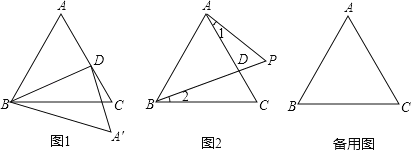
��1���ٵ�����15��ʱ����CBA'���� ����
��������ʾ��CBA'Ϊ�� ����
��2����ͼ2����P��BD�ӳ����ϣ��ҡ�1����2������
�ٵ�0��������60��ʱ����̽��AP��BP��CP֮���Ƿ����һ��������ϵ�����벢˵�����ɣ�
��BP��8��CP��n����CA'���� �������ú�n��ʽ�ӱ�ʾ��
���𰸡���1����30������60����2������2����BP��AP+CP�����ɼ���������8��2n
��������
��1���������ABC��60�����ó���ABD��60�������������۵��ó���A'BD��60�����������ɵó����ۣ�
��2�������жϳ���BP'C�ա�APC���ó�CP'��CP����BCP'����ACP�����жϳ���CPP'�ǵȱ������Σ��ó�PP'��CP��
���������BCP��120���������������BCA'��60��+�����жϳ���A'��C��P��ͬһ��ֱ���ϣ�����PA'��PC+CA'�����жϳ���ADP�ա�A'DP(SAS)���ó�A'P��AP�����ɵó����ۣ�
�⣺��1���ߡ�ABC�ǵȱ������Σ�
���ABC��60����
�ߡ�CBD������
���ABD����ABC����CBD��60��������
���۵�֪����A'BD����ABD��60��������
���CBA'����A'BD����CBD��60������������60����2����
�ٵ�����15��ʱ����CBA'��60����2����30����
�ʴ�Ϊ30����
��������ʾ��CBA'Ϊ60����2����
�ʴ�Ϊ60����2����
��2����BP��AP+CP�����ɣ���ͼ2������CP��

��BP��ȡһ��P'��ʹBP'��AP��
�ߡ�ABC�ǵȱ������Σ�
���ACB��60����BC��AC��
�ߡ�1����2������
���BP'C�ա�APC(SAS)��
��CP'��CP����BCP'����ACP��
���PCP'����ACP+��ACP'����BCP'+��ACP'����ACB��60����
��CP'��CP��
���CPP'�ǵȱ������Σ�
���CPB��60����PP'��CP��
��BP��BP'+PP'��AP+CP��
����ͼ3��
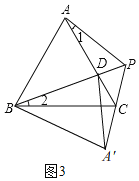
�ɢ�֪����BPC��60����
���BCP��180������BPC����PBC��180����60��������120��������
�ɣ�1��֪����CBA'��60����2����
���۵�֪��BA��BA'��
��BA��BC��
��BA'��BC��
���BCA'��![]() (180������CBA')��
(180������CBA')��![]() [180����(60����2��)]��60��+����
[180����(60����2��)]��60��+����
���BCP+��BCA'��120������+60��+����180����
���A'��C��P��ͬһ��ֱ���ϣ�
����PA'��PC+CA'��
���۵�֪��BA��BA'����ADB����A'DB��
��180������ADB��180������A'DB��
���ADP����A'DP��
��DP��DP��
���ADP�ա�A'DP(SAS)��
��A'P��AP��
�ɢ�֪��BP��AP+CP��
��BP��8��CP��n��
��AP��BP��CP��8��n��
��A'P��8��n��
��CA'��A'P��CP��8��n��n��8��2n��
�ʴ�Ϊ��8��2n��


 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����������ת����ת���У�ָ��λ�ù̶����������ε��������ȣ��ҷֱ��������1��2��3��

��1��С��ת��ת��һ�Σ���ת��ֹͣת��ʱ��ָ����ָ�����е������������ĸ���Ϊ________��
��2��С����ת��ת��һ�Σ���ת��ֹͣת��ʱ����¼��ָ����ָ�����е����֣�������ת��ת��һ�Σ���ת��ֹͣת��ʱ���ٴμ�¼��ָ����ָ�����е����֣�������������֮����3�ı����ĸ���(�û���״ͼ���б��ȷ������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ǡ�O�����ߣ��е�ֱ���A��B��ֱ��EFҲ�ǡ�O�����ߣ��е�ΪQ����PA��PB�ڵ�E��F����֪PA=12cm����P=40��
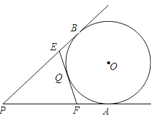
��1�����PEF���ܳ�.
��2�����EOF�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ѧ�е���������ϣ�Ҳ����������о�����������һ�������¿��Ի���ת��.���ν�Ͼ��ǰѳ������ѧ���ԡ�������ϵ��ֱ�۵ļ���ͼ�Ρ�λ�ù�ϵ���������ͨ������������������������������ͨ������˼ά������˼ά�Ľ�ϣ�����ʹ���������������������廯���Ӷ����Ż�����;����Ŀ��.
(1) ��˼��Ӧ�ã���֪m�� n��Ϊ��ʵ������m+n=2��![]() ����Сֵͨ����������˼����С���뵽����������Ĺ�����������:��ͼ�� AB=2��AC=1��BD=2��AC��AB��BD��AB����E���߶�AB�ϵĶ��㣬�Ҳ���˵��غϣ�����CE��DE����AE=m�� BE=n.
����Сֵͨ����������˼����С���뵽����������Ĺ�����������:��ͼ�� AB=2��AC=1��BD=2��AC��AB��BD��AB����E���߶�AB�ϵĶ��㣬�Ҳ���˵��غϣ�����CE��DE����AE=m�� BE=n.
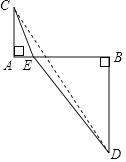
���ú�m�Ĵ���ʽ��ʾCE=_______�� �ú�n�Ĵ���ʽ��ʾDE= ;
�ھݴ���![]() ����Сֵ;
����Сֵ;
(2)�����Ӧ�ã����������ķ����������ʽ![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
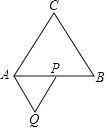
����Ŀ����ͼ���ȱ���ABC�ı߳�Ϊ6����P����ABC�ıߴ�A��B��C�˶�����APΪ�����ȱ���APQ���ҵ�Q��ֱ��AB�·�������P��Q�˶���ʹ��BPQ�ǵ���������ʱ����Q�˶�·�ߵij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺��y��z��2+��x��y��2+��z��x��2=��y+z��2x��2+��z+x��2y��2+��x+y��2z��2��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�AB=8����P�ڱ�CD�ϣ�tan��PBC=![]() ����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
��1����ͼ1������R���D�غ�ʱ����PQ�ij���
��2����ͼ2����̽���� ![]() �ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
�ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
��3����ͼ3������Q���߶�BP�ϣ���PQ=x��RM=y����y����x�ĺ�����ϵʽ����д�����Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �����߳�
�����߳�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������������
������������![]() ��
��![]() �����Լ��Ϊ
�����Լ��Ϊ![]() ����
����![]() �͵�
�͵�![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �����ĺ����ģ���
�����ĺ����ģ���![]() ����
����![]() ���ܳ�Ϊ________��
���ܳ�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
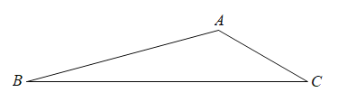
����Ŀ����ͼ������ABC�У���ABC![]() 15����AB
15����AB![]()
![]() ��BC
��BC![]() 2����ABΪֱ�DZ�����������ֱ����BAD���ҡ�BAD=90������BCΪб������������ֱ����BEC������DE��
2����ABΪֱ�DZ�����������ֱ����BAD���ҡ�BAD=90������BCΪб������������ֱ����BEC������DE��
��1����Ҫ��ȫͼ�Σ�
��2����DE����
��3��ֱ��д����ABC�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com