
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,
,![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() ,延长
,延长![]() 与
与![]() 的延长线交于
的延长线交于![]() ,
,![]() 在
在![]() 上,且
上,且![]() .
.
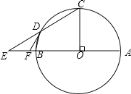
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连结OD,由CO⊥AB得∠E+∠C=90°,根据等腰三角形的性质由FE=FD,OD=OC得到∠E=∠FDE,∠C=∠ODC,于是有∠FDE+∠ODC=90°,则可根据切线的判定定理得到FD是⊙O的切线;
(2)连结AD,如图,利用圆周角定理,由AB为⊙O的直径得到∠ADB=90°,则∠A+∠ABD=90°,加上∠OBD=∠ODB,∠BDF+∠ODB=90°,则∠A=∠BDF,易得△FBD∽△FDA,根据相似的性质得![]() ,再在Rt△ABD中,根据正切的定义得到tan∠A=tan∠BDF=
,再在Rt△ABD中,根据正切的定义得到tan∠A=tan∠BDF=![]() =
=![]() ,于是可计算出DF=2,从而得到EF=2.
,于是可计算出DF=2,从而得到EF=2.
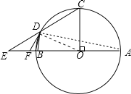
![]() 连结
连结![]() ,如图,
,如图,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
![]() 连结
连结![]() ,如图,
,如图,
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
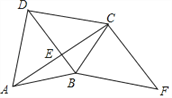
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,四边形ABEG、GEFH、HFCD都是边长为1的正方形.
(1)求证:△AEF∽△CEA;
(2)求证:∠AFB+∠ACB=45°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分) 如图,小明把一张边长为![]() 厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子,
厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子,

(1)如果要求长方体盒子的底面面积为![]() ,求剪去的小正方形边长为多少?
,求剪去的小正方形边长为多少?
(2)长方体盒子的侧面积是否可能为![]() ?为什么?
?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com