
【题目】如图1,矩形![]() 在坐标系中,
在坐标系中,![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,矩形
,矩形![]() 周长为18,面积为18.
周长为18,面积为18.

(1)求![]() 点坐标;
点坐标;
(2)如图2,![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,连
上,连![]() 、
、![]() ,若
,若![]() 于
于![]() ,
,![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
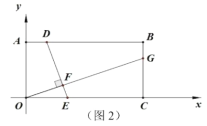
(3)如图3,在(2)的条件下,![]() 是
是![]() 中点,连
中点,连![]() 并延长
并延长![]() 至
至![]() ,连
,连![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
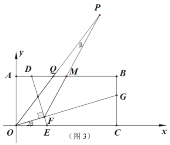
【答案】(1)B(6,3)(2)CG=2t(3)t=![]()
【解析】
(1)设B点坐标为(m,n),根据矩形周长和面积的值列方程组求解.
(2)作DH⊥OC于H,可证△DHE△OCG,由相似比可得CG=2HE=2AD.
(3)作MN⊥OC于N,交OG于K,连接OD,设DE与OQ交于点R.先证DMKF四点共圆,进而得出∠KFM=45![]() ,再导角推出OP是∠AOG的角平分线,然后可以导出△DRQ和△EOR均为等腰三角形,于是DE的长可用t表示出来.注意到∠AOD与∠NOK相等,可推出OD=DE,最后利用直角三角形AOD列勾股方程解出t的值.
,再导角推出OP是∠AOG的角平分线,然后可以导出△DRQ和△EOR均为等腰三角形,于是DE的长可用t表示出来.注意到∠AOD与∠NOK相等,可推出OD=DE,最后利用直角三角形AOD列勾股方程解出t的值.
(1)设B点坐标为(m,n)(m>n)
由题意可知:![]()
解得:![]() 或
或![]() (舍去)
(舍去)
∴B点坐标为(6,3).
(2)如图2,作DH⊥OC于H.
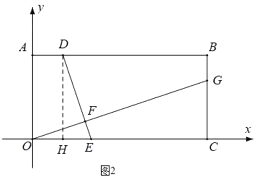
则∠DHE=90![]() ,
,
∴∠HDE+∠DEH=90![]() ,
,
∵DH⊥OG于F,
∴∠GOC+∠DEH=∠OFE=90![]() ,
,
∴∠HDE=∠COG,
∵∠OCG=90![]() =∠DHE,
=∠DHE,
∴△DHE△OCG,
∴![]()
∵B(6,3),
∴AB=OC=6,AO=DH=BC=3,
∴![]() =2,
=2,
∴CG=2HE,
∵D点横坐标为t,
∴OH=AD=t,
∴OE=2AD,
∴HE=OH=t,
∴CG=2HE=2t.
(3)如图3,作MN⊥OC于N,交OG于K,连接OD.
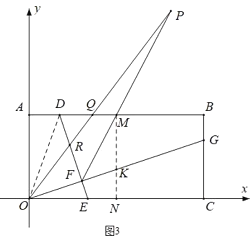
∵M为AB中点,
∴AM=BM=ON=CN=AO=BC=MN=3,KN=![]() CG=t,
CG=t,
∴KN=AD,所以DM=KM,
∵∠DFK=∠DMK=90![]() ,
,
∴DFKM四点共圆,
∴∠DFM=∠KFM=45![]() ,
,
∵∠KFM=∠OPF+∠FOP,
∴∠FOP+![]() =45
=45![]() ,
,
∴2∠FOP+2![]() =90°,
=90°,
∵∠AOC=90![]() ,
,
∴∠AOQ+∠FOP+∠COG=∠AOQ+∠FOP+2![]() =90
=90![]() ,
,
∴∠AOQ=∠FOP,
∵∠AOQ=∠OFR=90![]() ,
,
∴∠ORF=∠OQA,
∵∠ORF=∠DRQ,∠OQA=∠ROE,
∴∠DRQ=∠OQA,∠ROE=∠ORF,
∴DR=DQ=![]() ,RE=OE=2t,
,RE=OE=2t,
∴DE=DR+RE=![]() +2t,
+2t,
∵tan∠AOD=![]() =tan∠NOK,
=tan∠NOK,
∴∠AOD=∠NOK,
∵∠AOD+∠DOE=∠NOK+∠OEF=90![]() ,
,
∴∠DOE=∠OEF,
∴OD=DE=![]() +2t,
+2t,
在Rt△AOD中:OA2+AD2=OD2,
∴9+t2=(![]() +2t)2,
+2t)2,
解得t=![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
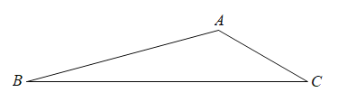
【题目】如图,在△ABC中,∠ABC![]() 15°,AB
15°,AB![]()
![]() ,BC
,BC![]() 2,以AB为直角边向外作等腰直角△BAD,且∠BAD=90°;以BC为斜边向外作等腰直角△BEC,连接DE.
2,以AB为直角边向外作等腰直角△BAD,且∠BAD=90°;以BC为斜边向外作等腰直角△BEC,连接DE.
(1)按要求补全图形;
(2)求DE长;
(3)直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
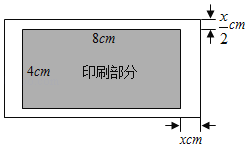
【题目】如图,印刷一张矩形的包装纸,印刷部分的长为8cm,宽为4cm,上下空白宽各![]() cm,左右空白宽各xcm,四周空白处的面积为Scm2.
cm,左右空白宽各xcm,四周空白处的面积为Scm2.
(1)求S与x的关系式;
(2)当四周空白处的面积为18cm2时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建火车站站前广场需要绿化的面积为46000米2,施工队在绿化了22000米2后,将每天的工作量增加为原来的1.5倍,结果提前4天完成了该项绿化工程.
(1)该项绿化工程原计划每天完成多少米2?
(2)该项绿化工程中有一块长为20米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56米2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿虚线用剪刀平均分成四个小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿虚线用剪刀平均分成四个小长方形,然后按图②的形状拼成一个正方形.
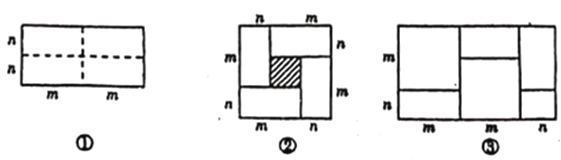
(1)图②中阴影部分的正方形的边长为
(2)观察图②,三个代数式![]() 之间的数量关系式是 .
之间的数量关系式是 .
(3)观察图③,写出一个代数恒等式: .
(4)在下面的虚线框中画出一个几何图形,使它的面积能表示成![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com