
【题目】如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿虚线用剪刀平均分成四个小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿虚线用剪刀平均分成四个小长方形,然后按图②的形状拼成一个正方形.
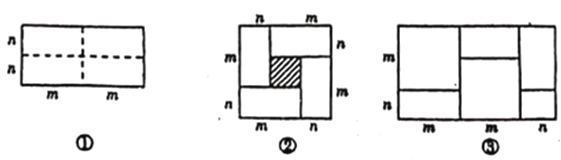
(1)图②中阴影部分的正方形的边长为
(2)观察图②,三个代数式![]() 之间的数量关系式是 .
之间的数量关系式是 .
(3)观察图③,写出一个代数恒等式: .
(4)在下面的虚线框中画出一个几何图形,使它的面积能表示成![]()

【答案】(1)m-n;(2)(m+n)2-4mn=(m-n)2;(3)(2m+n)(m+n)=2m(m+n)+n(m+n);(4)见解析.
【解析】
(1)由图形可以得出阴影部分的边长即小长方形的长减去小长方形的宽;
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式(m+n)2、(m-n)2、mn之间的等量关系.
(3)利用两种不同的方法表示出大矩形的面积即可得出等式.
(4)画出边长分别为(m+n)和(m+2n)长方形即可.
(1)图②中的阴影部分的正方形边长为m-n;
(2)(m+n)2-4mn=(m-n)2;
(3)(2m+n)(m+n)=2m(m+n)+n(m+n).
(4)如图所示:

故答案为:(1)(m-n)2、(2)(m+n)2-4mn=(m-n)2、(3)(2m+n)(m+n)=2m(m+n)+n(m+n).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
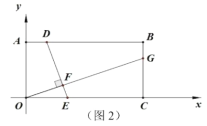
【题目】如图1,矩形![]() 在坐标系中,
在坐标系中,![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,矩形
,矩形![]() 周长为18,面积为18.
周长为18,面积为18.

(1)求![]() 点坐标;
点坐标;
(2)如图2,![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,连
上,连![]() 、
、![]() ,若
,若![]() 于
于![]() ,
,![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
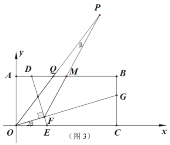
(3)如图3,在(2)的条件下,![]() 是
是![]() 中点,连
中点,连![]() 并延长
并延长![]() 至
至![]() ,连
,连![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
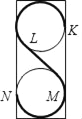
【题目】如图,字母S由两条圆弧KL、MN和线段LM组成,这两条圆弧每一条都是一个半径为1的圆的圆周的![]() ,线段LM与两个圆相切.K和N分别是两个圆的切点,则线段LM的长为_________.
,线段LM与两个圆相切.K和N分别是两个圆的切点,则线段LM的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展学生安全知识竞赛.现抽取部分学生的竞赛成绩(满分为100分,得分均为整数)进行统计,绘制了图中两幅不完整的统计图.根据图中信息,回答下列问题:
(1)a= ,n= ;
(2)补全频数分布直方图;
(3)该校共有2000名学生.若成绩在80分以上的为优秀,请你估计该校成绩优秀的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
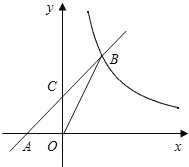
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
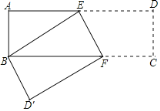
A.6cm2B.8 cm2C.10 cm2D.12 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
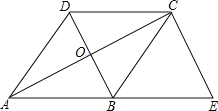
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若AB=5, BD=6时,求△ACE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=58°,求∠BDF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com