
【题目】某校开展学生安全知识竞赛.现抽取部分学生的竞赛成绩(满分为100分,得分均为整数)进行统计,绘制了图中两幅不完整的统计图.根据图中信息,回答下列问题:
(1)a= ,n= ;
(2)补全频数分布直方图;
(3)该校共有2000名学生.若成绩在80分以上的为优秀,请你估计该校成绩优秀的学生人数.

【答案】(1)75,54;
(2)补全频数分布直方图见解析;
(3)估计该校成绩优秀的学生人数是900人.
【解析】试题分析:(1)根据A组的人数是30人,所占的百分比是10%,据此即可求得抽取的总人数,然后利用百分比的计算方法求得B组的人数,进而求得a和E组的人数,利用360乘以E组对应的比例求得n的值;(2)利用(1)的结果可以补全直方图;(3)利用总人数乘以对应的比例即可求解.
试题解析:(1)抽取的总人数是30÷10%=300(人),
则B组的人数是300×20%=60(人),
a=300×25%=75,
E组的人数是30030607590=45(人)
n=360×![]() =54.
=54.
故答案是:75,54;
(2)
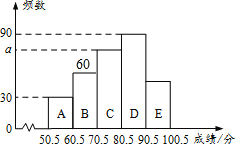 ;
;
(3)估计该校成绩优秀的学生人数是:2000×![]() =900(人).
=900(人).
答:估计该校成绩优秀的学生人数是900人。


科目:初中数学 来源: 题型:
【题目】如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5米的速度收绳子.
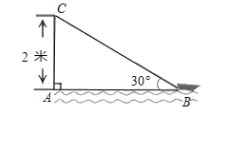
问:(1)未开始收绳子的时候,图中绳子BC的长度是多少米?
(2)收绳2秒后船离岸边多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.
(1)求证:四边形ABEF是菱形;
(2)若AB=5,BF=8,AD=![]() ,则ABCD的面积是______.
,则ABCD的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
![]()
请写出AB中点M对应的数。
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动。设两只电子蚂蚁在数轴上的C点相遇,你知道C点对应的数是多少吗?
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动。设两只电子蚂蚁在数轴上的D点相遇,你知道D点对应的数是多少吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象与一次函数y=﹣x﹣1的图象的一个交点为A(﹣2,a).
的图象与一次函数y=﹣x﹣1的图象的一个交点为A(﹣2,a).
(1)求反比例函数的表达式;
(2)请直接写出不等式![]() >﹣x﹣1的解集;
>﹣x﹣1的解集;
(3)若一次函数=﹣x﹣1与x轴交于点B,与y轴交于点C,点P是反比例函数y=![]() 图象上一点,且S△BOP=4S△OBC,求点P的坐标.
图象上一点,且S△BOP=4S△OBC,求点P的坐标.
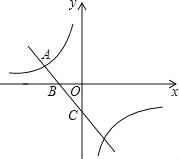
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费。下表是该市民居民“一户一表”生活用水阶梯式计费价格表的部分信息:

(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费)
已知小王家2012年4月用水20吨,交水费66元,5月份用水25吨,交水费91元。
(1)求a,b的值;
(2)随着夏天的到来,用水量将增加。为了节省开支。小王计划把6月份的水费控制在不超过家庭月收入的2%,若小王家的月收入为9200元,则小王家6月份最多能用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求铁架垂直管CE的长(结果精确到0.01米).
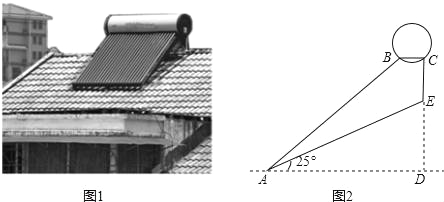
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线y=![]() x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
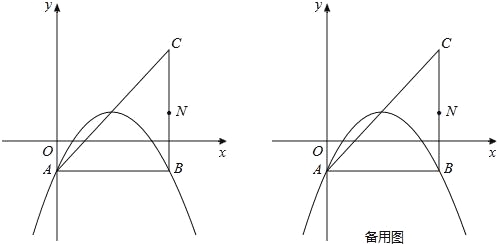
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com