
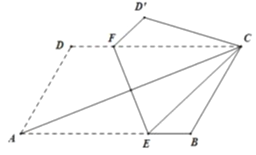
【题目】如图,将平行四边形![]() 沿
沿![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() 到
到![]() 的距离为____________.
的距离为____________.
【答案】![]()
【解析】分析:过点C作CM⊥AB的延长线于点M,根据翻折的性质,设AE=x,CE=x,BE=6-x,EM=8-x,在△CEM中,利用勾股定理列出方程即可求出x的值.然后算出三角形CBE的面积,根据等面积法即可求出点B到CE的距离.
详解:作CM⊥AB于M,如图所示:
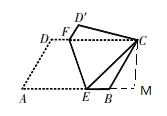
则∠M=90°,
∵四边形ABCD是平行四边形,
∴BC=AD=4,BC∥AD,
∴∠CBM=∠A=60°,
∴∠BCM=30°,
∴BM=![]() BC=4×
BC=4×![]() =2.
=2.
在Rt△BMC中,根据勾股定理可得CM=2![]() .
.
设AE=x,则CE=x,BE=6-x,EM=8-x,
∵CE2=CM2+EM2,
∴x2=(2![]() )2+(8-x)2,
)2+(8-x)2,
解得:x=![]() ,
,
∴CE=![]() ,BE=6-
,BE=6-![]() =
=![]() ,
,
∴S△CBE=![]() .
.
∴点B到CE的距离= S△CBE÷CE×2=![]() .
.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(1,5)在函数![]() (x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )
(x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )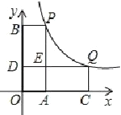
A. 先增大后减小 B. 先减小后增大
C. 先减小后增大再减小 D. 先增大后减小再增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元. 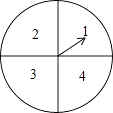
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 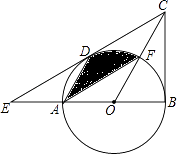
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个棱长为![]() 的正方体的每个面等分成
的正方体的每个面等分成![]() 个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去
个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去![]() 个小正方体),所得到的几何体的表面积是( )
个小正方体),所得到的几何体的表面积是( )

A. 78 B. 72 C. 54 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。
的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。

(1)求两个函数的解析式;
(2)观察图像,写出当x为何值时y1>y2?
(3)C、D分别是反比例函数![]() 第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标.
第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰三角形ABO的底边OA在x轴上,顶点B在反比例函数y= ![]() (x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=
(x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y= ![]() (x>0)的图象上滑动,但点O始终位于原点.
(x>0)的图象上滑动,但点O始终位于原点.
(1)如图①,若点A的坐标为(6,0),求点B的坐标;
(2)当点A移动到什么位置时,三角形ABO变成等腰直角三角形,请说明理由;
(3)在(2)中,如图②,△PA1A是等腰直角三角形,点P在反比例函数y= ![]() (x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
(x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com