
【题目】如图,在平面直角坐标系中,等腰三角形ABO的底边OA在x轴上,顶点B在反比例函数y= ![]() (x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=
(x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y= ![]() (x>0)的图象上滑动,但点O始终位于原点.
(x>0)的图象上滑动,但点O始终位于原点.
(1)如图①,若点A的坐标为(6,0),求点B的坐标;
(2)当点A移动到什么位置时,三角形ABO变成等腰直角三角形,请说明理由;
(3)在(2)中,如图②,△PA1A是等腰直角三角形,点P在反比例函数y= ![]() (x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
(x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
【答案】
(1)
解:如图①,过点B作BC⊥x轴于点C,
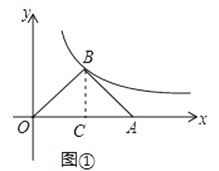
∵OB=AB,
∴OC=AC,点A移动到什么位置时,三角形ABO变成等腰直角三角形,
∵点A的坐标为(6,0),
∴OC= ![]() OA=3,
OA=3,
∵顶点B在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴y= ![]() =4,
=4,
∴点B的坐标为:(3,4)
(2)
解:点A移动到(4 ![]() ,0)时,△ABO变成等腰直角三角形.
,0)时,△ABO变成等腰直角三角形.
理由:如图②,过点B作BC⊥x轴于点C,
∵△AOB是等腰直角三角形,
∴BC=OC= ![]() OA,
OA,
设点B(a,a),
∵顶点B在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴a= ![]() ,
,
解得:a=±2 ![]() (负值舍去),
(负值舍去),
∴OC=2 ![]() ,
,
∴OA=2OC=4 ![]() ,
,
∴点A移动到(4 ![]() ,0)时,△ABO变成等腰直角三角形
,0)时,△ABO变成等腰直角三角形
(3)
解:如图②,过点P作PD⊥x轴于点D,

∵△PA1A是等腰直角三角形,
∴PD=AD,
设AD=b,则点P(4 ![]() +b,b),
+b,b),
∵点P在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴b= ![]() ,
,
解得:b1=2 ![]() ﹣2
﹣2 ![]() ,b2=﹣2
,b2=﹣2 ![]() ﹣2
﹣2 ![]() (舍去),
(舍去),
∴AA1=2b=4 ![]() ﹣4
﹣4 ![]() ,
,
∴OA1=OA+AA1=4 ![]() ,
,
∴点A1的坐标为:(4 ![]() ,0).
,0).
【解析】(1)首先过点B作BC⊥x轴于点C,由等腰三角形的三线合一,可得OC=AC=3,然后由顶点B在反比例函数y= ![]() (x>0)的图象上,求得点B的坐标;(2)首先由等腰直角三角形的性质,可得OC=BC,然后由顶点B在反比例函数y=
(x>0)的图象上,求得点B的坐标;(2)首先由等腰直角三角形的性质,可得OC=BC,然后由顶点B在反比例函数y= ![]() (x>0)的图象上,求得点B的坐标,继而求得点A的坐标;(3)首先过点P作PD⊥x轴于点D,易得AD=PD,则可设AD=b,则点P(4
(x>0)的图象上,求得点B的坐标,继而求得点A的坐标;(3)首先过点P作PD⊥x轴于点D,易得AD=PD,则可设AD=b,则点P(4 ![]() +b,b),又由点P在反比例函数y=
+b,b),又由点P在反比例函数y= ![]() (x>0)的图象上,求得b的值,继而求得答案.
(x>0)的图象上,求得b的值,继而求得答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一组数据7,2,5,4,2的方差为a,若再增加一个数据4,这6个数据的方差为b,则a与b的大小关系是( )
A. a>b B. a=b C. a<b D. 以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=![]() .
.
![]()
利用数轴,根据数形结合思想,回答下列问题:
(1)数轴上表示2和6两点之间的距离是_____ ,数轴上表示1和![]() 的两点之间的距离为__________
的两点之间的距离为__________
(2)数轴上表示![]() 和1两点之间的距离为_____,数轴上表示
和1两点之间的距离为_____,数轴上表示![]() 和
和![]() 两点之间的距离为_________
两点之间的距离为_________
(3)若![]() 表示一个实数,且
表示一个实数,且![]() ,化简
,化简![]() ,
,
(4)![]() 的最小值为_______ ,
的最小值为_______ ,
![]() 的最小值为__________ .
的最小值为__________ .
(5)![]() 的最大值为__________
的最大值为__________
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).
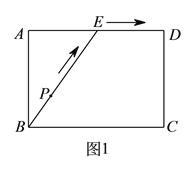

A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究. (操作)如图,在矩形ABCD中,AD=6,AB=4,点P是BC边上一点,现将△APB沿AP对折,得△APM,显然点M位置随P点位置变化而发生改变
(问题)试求下列几种情况下:点M到直线CD的距离
(1)∠APB=75°;
(2)P与C重合;
(3)P是BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究. (操作)如图,在矩形ABCD中,AD=6,AB=4,点P是BC边上一点,现将△APB沿AP对折,得△APM,显然点M位置随P点位置变化而发生改变
(问题)试求下列几种情况下:点M到直线CD的距离
(1)∠APB=75°;
(2)P与C重合;
(3)P是BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动。设该机器人每秒前进或后退1步,并且每步的距离为一个单位长度,![]() 表示第n秒时机器人在数轴上位置所对应的数。则下列结论中正确的有______.(只需填入正确的序号)
表示第n秒时机器人在数轴上位置所对应的数。则下列结论中正确的有______.(只需填入正确的序号)
①![]() ②
②![]() ③
③![]() ④
④![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com