
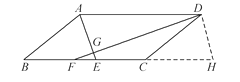
【题目】已知:如图,在ABCD中,∠ADC,∠DAB的平分线DF,AE分别与线段BC相交于点F,E,DF与AE相交于点G.
(1)求证:AE⊥DF;
(2)若AD=10,AB=6,AE=4,求DF的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=![]() (∠ADC+∠DAB)=90°,即可求出结论;
(∠ADC+∠DAB)=90°,即可求出结论;
(2)过点D作DH∥AE,交BC的延长线于点H,得到平行四边形AEHD,求出DH=AE=4,EH=AD=10,根据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出BF、FE、FH的长,根据勾股定理即可求出答案.
试题解析:(1)∵在ABCD中,AB∥CD,
∴∠ADC+∠DAB=180°,
∵DF,AE分别是∠ADC,∠DAB的平分线,
∴∠ADF=∠CDF=![]() ∠ADC,∠DAE=∠BAE=
∠ADC,∠DAE=∠BAE=![]() ∠DAB,
∠DAB,
∴∠ADF+∠DAE=![]() (∠ADC+∠DAB)=90°,
(∠ADC+∠DAB)=90°,
∴∠AGD=90°,即AE⊥DF;
(2)如图,过点D作DH∥AE,交BC的延长线于点H,则四边形AEHD是平行四边形,且FD⊥DH,
∴DH=AE=4,EH=AD=10,
∵在ABCD中,AD∥BC,∴∠ADF=∠CFD,∠DAE=∠BEA,
∴∠CDF=∠CFD,∠BAE=∠BEA,
∴DC=FC,AB=EB,
在ABCD中,AD=BC=10,AB=DC=6,∴CF=BE=6,BF=BC-CF=10-6=4,
∴FE=BE-BF=6-4=2,∴FH=FE+EH=12,
在Rt△FDH中,DF=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(1,5)在函数![]() (x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )
(x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )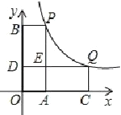
A. 先增大后减小 B. 先减小后增大
C. 先减小后增大再减小 D. 先增大后减小再增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。
的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。

(1)求两个函数的解析式;
(2)观察图像,写出当x为何值时y1>y2?
(3)C、D分别是反比例函数![]() 第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标.
第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰三角形ABO的底边OA在x轴上,顶点B在反比例函数y= ![]() (x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=
(x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y= ![]() (x>0)的图象上滑动,但点O始终位于原点.
(x>0)的图象上滑动,但点O始终位于原点.
(1)如图①,若点A的坐标为(6,0),求点B的坐标;
(2)当点A移动到什么位置时,三角形ABO变成等腰直角三角形,请说明理由;
(3)在(2)中,如图②,△PA1A是等腰直角三角形,点P在反比例函数y= ![]() (x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
(x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)过多边形的一个顶点的所有对角线的条数与这些对角线分多边形所得的三角形个数的和为![]() ,求这个多边形的边数;
,求这个多边形的边数;
(2)过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为![]() 吗?若能,请求出这个多边形的边数;若不能,请说明理由.
吗?若能,请求出这个多边形的边数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰三角形ABO的底边OA在x轴上,顶点B在反比例函数y= ![]() (x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y=
(x>0)的图象上,当底边OA上的点A在x轴的正半轴上自左向右移动时,顶点B也随之在反比例函数y= ![]() (x>0)的图象上滑动,但点O始终位于原点.
(x>0)的图象上滑动,但点O始终位于原点.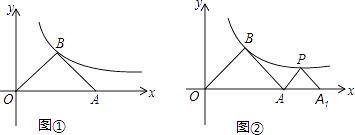
(1)如图①,若点A的坐标为(6,0),求点B的坐标;
(2)当点A移动到什么位置时,三角形ABO变成等腰直角三角形,请说明理由;
(3)在(2)中,如图②,△PA1A是等腰直角三角形,点P在反比例函数y= ![]() (x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
(x>0)的图象上,斜边A1A在x轴上,求点A1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com