
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
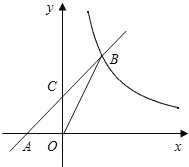
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
【答案】解:(1)由A(﹣2,0),得OA=2;
∵点B(2,n)在第一象限内,S△AOB=4,∴![]() OAn=4。∴n=4。∴点B的坐标是(2,4)。
OAn=4。∴n=4。∴点B的坐标是(2,4)。
设该反比例函数的解析式为![]() ,
,
将点B的坐标代入,得![]() ,∴m=8。
,∴m=8。
∴反比例函数的解析式为:![]() 。
。
设直线AB的解析式为y=kx+b(k≠0),
将点A,B的坐标分别代入,得![]() ,解得,
,解得,![]() 。
。
∴直线AB的解析式为y=x+2。
(2)在y=x+2中,令x=0,得y=2,∴点C的坐标是(0,2)。∴OC=2。
∴S△OCB=![]() OC×2=
OC×2=![]() ×2×2=2。
×2×2=2。
【解析】
试题(1)先由A(﹣2,0),得OA=2,点B(2,n),S△AOB=4,得![]() OAn=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为
OAn=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为![]() ,可得反比例函数的解析式为:
,可得反比例函数的解析式为:![]() ;再把A(﹣2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2。
;再把A(﹣2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2。
(2)把x=0代入直线AB的解析式y=x+2得y=2,即OC=2,可得S△OCB=![]() OC×2=
OC×2=![]() ×2×2=2。
×2×2=2。


科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y=![]() (1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1,将C1向左平移2个单位长度,得曲线C2,请在图中画出C2,并直接写出C1平移到C2处所扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则,等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化作整式与真分式的和的形式.
如:![]() ;
;![]()
(1)下列分式中,属于真分式的是__________(填序号);
①![]() ②
②![]() ③
③![]() ④
④![]()
(2)将假分式![]() 化为整式与真分式的和的形式:
化为整式与真分式的和的形式:![]() __________;若假分式
__________;若假分式![]() 的值为正整数,则整数
的值为正整数,则整数![]() 的值为__________;
的值为__________;
(3)请你写出假分式![]() 化成整式与真分式的和的形式的完整过程.
化成整式与真分式的和的形式的完整过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,马路的两边![]() ,
,![]() 互相平行,线段
互相平行,线段![]() 为人行横道,马路两侧的
为人行横道,马路两侧的![]() ,
,![]() 两点分别表示车站和超市.
两点分别表示车站和超市.![]() 与
与![]() 所在直线互相平行,且都与马路的两边垂直,马路宽
所在直线互相平行,且都与马路的两边垂直,马路宽![]() 米,
米,![]() ,
,![]() 相距
相距![]() 米,
米,![]() ,
,![]() .
.

(1)求![]() 与
与![]() 之间的距离;
之间的距离;
(2)某人从车站![]() 出发,沿折线
出发,沿折线![]() 去超市
去超市![]() .求他沿折线
.求他沿折线![]() 到达超市比直接横穿马路多走多少米.
到达超市比直接横穿马路多走多少米.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为![]() ,宽为
,宽为![]() 的长方形,沿虚线用剪刀平均分成四个小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿虚线用剪刀平均分成四个小长方形,然后按图②的形状拼成一个正方形.
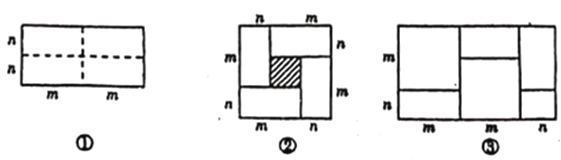
(1)图②中阴影部分的正方形的边长为
(2)观察图②,三个代数式![]() 之间的数量关系式是 .
之间的数量关系式是 .
(3)观察图③,写出一个代数恒等式: .
(4)在下面的虚线框中画出一个几何图形,使它的面积能表示成![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
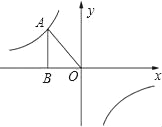
【题目】如图,已知反比例函数y=![]() (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并解答问题
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为![]() ,可设
,可设![]() ,
,
则![]()
∵对任意![]() 上述等式均成立,
上述等式均成立,
∴![]() 且
且![]() ,∴
,∴![]() ,
,![]()
∴![]()
这样,分式![]() 被拆分成了一个整式
被拆分成了一个整式![]() 与一个分式
与一个分式![]() 的和
的和
解答:(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式
拆分成一个整式与一个分式(分子为整数)的和的形式
(2)求出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com