
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是(请将所有正确结论的序号都填上). 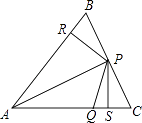
【答案】①②④
【解析】解:①∵PR⊥AB,PS⊥AC,PR=PS, ∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2﹣PR2 , AS2=AP2﹣PS2 ,
∵AD=AD,PR=PS,
∴AR=AS,∴①正确;
②∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,∴②正确;
③在Rt△BRP和Rt△QSP中,只有PR=PS,
不满足三角形全等的条件,故③错误;
④如图,连接RS,与AP交于点D.
在△ARD和△ASD中,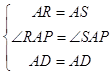 ,
,
所以△ARD≌△ASD.
∴RD=SD,∠ADR=∠ADS=90°.
所以AP垂直平分RS,故④正确.
故答案为:①②④.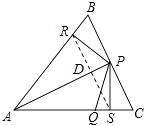
根据角平分线性质即可推出①,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP∥AB即可;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断△BRP≌△QSP;连接RS,与AP交于点D,先证△ARD≌△ASD,则RD=SD,∠ADR=∠ADS=90°.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:

(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=2(x﹣3)2+2图象向左平移6个单位,再向下平移2个单位后,所得图象的函数表达式是( )
A.y=2(x-9)2B.y=2(x+3)2
C.y=2(x+3)2+4D.y=2(x-9)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( ) 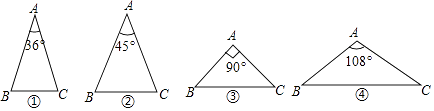
A.①③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母). 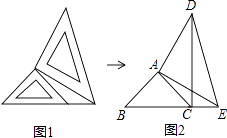
(1)你找到的全等三角形是:;
(2)证明: ![]() ﹣
﹣ ![]() ÷
÷ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 过任意一点可作已知直线的一条平行线
B. 同一平面内两条不相交的直线是平行线
C. 在同一平面内,过一点只能画一条直线与已知直线垂直
D. 在同一平面内,经过直线外一点有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
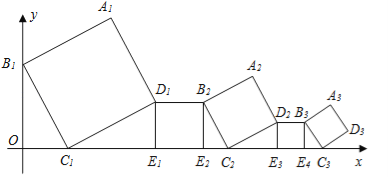
【题目】在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com