���㣺Բ���ۺ���,ȫ�������ε��ж�������,��������λ�߶���,���ε�����,������λ�߶���,���ߵ��ж�������,���߳�����,���������ε��ж�������
ר�⣺�ۺ���
��������1�����þ��ε����ʣ���֤��AHE�ա�CGE���Ϳɽ�����⣮
��2������OH��OE��OG����ͼ2��������������λ�߶�����������λ�߶����ɵ�OE=
AD=
��AH+BG��������AH+BG=AD����֤AD��BC���ǡ�O�����ߣ��������߳������ɵ�HA=HF����AHO=��FHO��GB=GF����BGO=��FGO��Ȼ�����ƽ���ߵ����ʿɵá�AHG+��BGH=180�㣬�ɴ˿�֤����AHO=��BOG���Ӷ��ɵá�HAO�ס�OBG��Ȼ���������������ε����ʼ�������߶�AH�ij��ȣ�
��3���ɣ�2���ѵã�AH��OE��HA=HF��GB=GF��OE=
��AH+BG�����Ӷ��ɵá�BOE=��BAD=90�㼴EO��AB��OE=
��AH+BG��=
��HF+FG��=
HG���ɴ˿ɵ���GHΪֱ����Բ��ֱ��AB���У�
����⣺��1����ͼ1��
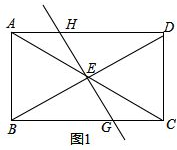
���ı���ABCD�Ǿ��Σ�
��EA=EC��AD��BC��
���HAE=��GCE��
�ڡ�AHE�͡�CGE�У�
| | ��HAE=��GCE | | AE=CE | | ��AEH=��CEG |
| |
��
���AHE�ա�CGE��ASA����
���AEH���CEG���ڵ�E�����ĶԳƣ�AH=CG��EH=EG��
�ʴ�Ϊ���١�AEH���CEG���ڵ�E�����ĶԳƣ���AH=CG��
��2����1������OH��OE��OG����ͼ2��
���ı���ABCD�Ǿ��Σ�
��AD��BC����BAD=��ABC=90�㣬BE=DE��
��BO=AO��BE=DE��
��OE=
AD��
��AD��BC��BO=AO��HE=GE��
��OE=
��AH+BG��=
AD����AH+BG=AD=4��
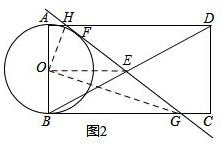
��ABΪ��O��ֱ����
��AD��BC���ǡ�O�����ߣ�
��GH���O����
��HA=HF����AHO=��FHO��GB=GF����BGO=��FGO��
��AD��BC��
���AHG+��BGH=180�㣬
��2��AHO+2��BGO=180�㣬
���AHO+��BGO=90�㣮
�ߡ�BOG+��BGO=90�㣬
���AHO=��BOG��
�֡ߡ�HAO=��OBC=90�㣬
���HAO�ס�OBG��
��
=
����AH•BG=AO•BO��
��AH•��4-AH��=1��1=1��
��ã�AH=2+
��AH=2-
��
���߶�AH�ij���Ϊ2+
��2-
��
��2������G��GP��AD�ڵ�P����ͼ2��
����PD=GC=AH��
�������߳������ɵã�AH=FH��GF=GB��
��AH=x����GC=PD=x��BG=AP=4-x��GH=FH+FG=x+4-x=4��
��Rt��GPH��
��GH=4��GP=AB=2��
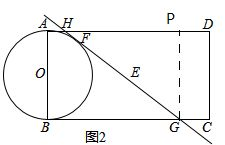
��PH=
=2
��
����H�ڵ�P�����ʱ��
����PH=4-2x=2
��
��ã�x=2-
��
����H�ڵ�P���ұ�ʱ��
����PH=2x-4=2
��
��ã�x=2+
��
�����������߶�AH�ij���Ϊ2+
��2-
��
��3����GHΪֱ����Բ��ֱ��AB���У�
���ɣ���AH��OE��
���BOE=��BAD=90�㣬��EO��AB��
��HA=HF��GB=GF��
��OE=
��AH+BG��=
��HF+FG��=
HG��
����GHΪֱ����Բ��ֱ��AB���У�
������������Ҫ���������ߵ��ж������ʡ����߳����������ε����ʡ�ȫ�������ε��ж������ʡ����������ε��ж������ʡ���������λ�߶�����������λ�߶�����֪ʶ���ۺ��ԱȽ�ǿ����֤��AH+BG=AD����HAO�ס�OBG�ǽ���ڣ�2��С��Ĺؼ���







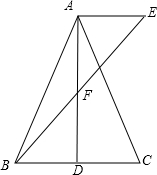 ��ͼ���ڡ�ABC�У�AB=AC��AD��BC�ڵ�D��FΪAD���е㣬AE��BC�ҽ�BF���ӳ�����E����AD=9��BC=12����BE�ij���
��ͼ���ڡ�ABC�У�AB=AC��AD��BC�ڵ�D��FΪAD���е㣬AE��BC�ҽ�BF���ӳ�����E����AD=9��BC=12����BE�ij��� ��MN�ѡ�O�ֳ�1��3������OM��ON����MN���е�A��AB��ON����
��MN�ѡ�O�ֳ�1��3������OM��ON����MN���е�A��AB��ON����
