
【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(![]() 取1.732,结果保留整数)
取1.732,结果保留整数)

科目:初中数学 来源: 题型:
【题目】(教材回顾)
七上教材有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)
四边形有4个顶点,如果在它的内部再画n个点,并以这(n+4)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)
为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
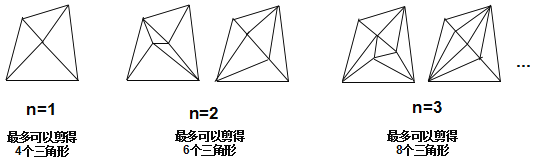
(问题解决)
(1)当四边形内有4个点时,最多剪得的三角形个数为______________;
(2)你发现的变化规律是:四边形内的点每增加1个,最多剪得的三角形增加______个;
(3)猜想:当四边形内点的个数为n时,最多可以剪得_______________个三角形;像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
请你尝试用归纳的方法探索4+6+8+10+…+2n+(2n+2)的和是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A向右移动1个单位得到B,点B向右移动(n+1)个单位得到点C,点C向右移动(n+2)(n为正整数)个单位得到点D,点A,B,C,D分别表示有理数a,b,c,d.
(1)当n=1时,B,C两点的距离为 个单位,C,D两点的距离为 个单位;
(2)当a=-10,n=1时,若A,B两点以2个单位长度/秒的速度向右匀速运动,同时C,D两点以1个单位长度/秒的速度向左匀速运动,并设运动时间为t秒,若A,B两点都运动在C,D两点之间(不与C,D两个点重合)时,求t的取值范围;
(3)a,b,c,d四个数的积为正数,且这四个数的和与其中的两个数的和相等,a为整数.若n分别取1,2,3,4……,50时,对应的a的值分贝记为a1,a2,a3,……,a50,则a1+a2+a3+……+a50=
查看答案和解析>>
科目:初中数学 来源: 题型:
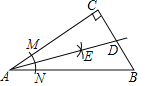
【题目】如图,在Rt△ABC中,∠C=90°,以原点A为圆心,适当的长为半径画弧,分别交AC,AB于点M,N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点E,作射线AE交BC于点D,若BD=5,AB=15,△ABD的面积30,则AC+CD的值是( )
MN的长为半径画弧,两弧交于点E,作射线AE交BC于点D,若BD=5,AB=15,△ABD的面积30,则AC+CD的值是( )
A. 16B. 14C. 12D. 5![]() +4
+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
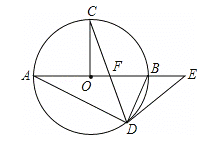
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若tanA=![]() ,探究线段AB和BE之间的数量关系,并证明;
,探究线段AB和BE之间的数量关系,并证明;
(3)在(2)的条件下,若OF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
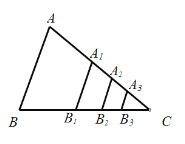
【题目】如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为![]() ,再分别取A1C、B1C的中点A2、B2,取A2C、B2C的中点A3、B3,依次取下去…利用这一图形,能直观地计算出
,再分别取A1C、B1C的中点A2、B2,取A2C、B2C的中点A3、B3,依次取下去…利用这一图形,能直观地计算出![]() ( )
( )
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字:
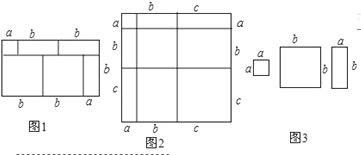
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,
①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.即2a2+5ab+2b2=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com