
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠。点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积。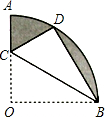
解:连接OD.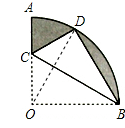
根据折叠的性质,CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等边三角形,
∴∠DBO=60°,
∴∠CBO= ∠DBO=30°,
∠DBO=30°,
∵∠AOB=90°,
∴OC=OB•tan∠CBO=6× =
= ,
,
∴S△BDC=S△OBC= ×OB×OC=
×OB×OC= ×6×2
×6×2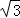 =6
=6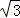 ,S扇形AOB=
,S扇形AOB=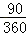 π×62=9π,
π×62=9π,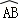 =
=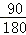 π×6=3π,
π×6=3π,
∴整个阴影部分的周长为:AC+CD+BD+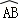 =AC+OC+OB+
=AC+OC+OB+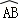 =OA+OB+
=OA+OB+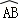 =6+6+3π=12+3π;
=6+6+3π=12+3π;
整个阴影部分的面积为:S扇形AOB﹣S△BDC﹣S△OBC=9π﹣6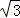 ﹣6
﹣6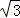 =9π﹣12
=9π﹣12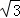 .
. 
解析试题分析:首先连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,继而求得OC的长,即可求得△OBC与△BCD的面积,又由在扇形OAB中,∠AOB=90°,半径OA=6,即可求得扇形OAB的面积与 的长,继而求得整个阴影部分的周长和面积.
的长,继而求得整个阴影部分的周长和面积.
考点:翻折变换(折叠问题);等边三角形的判定与性质;弧长的计算;扇形面积的计算;解直角三角形.
点评:此题考查了折叠的性质、扇形面积公式、弧长公式以及直角三角形的性质.此题难度适中,注意数形结合思想的应用,注意辅助线的作法.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
(本小题满分10分)如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.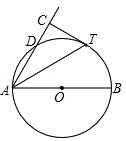
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,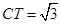 ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(10分)如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF= AC.
AC.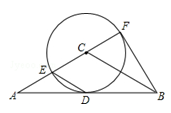
(1)求∠ACB的度数;
(2)若AC=8,求△ABF的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:填空题
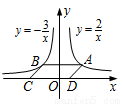
如图,点A是反比例函数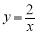 (
(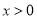 )的图象上任意一点,AB∥x轴交反比例函数
)的图象上任意一点,AB∥x轴交反比例函数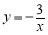 的图象于点B,以AB为边作
的图象于点B,以AB为边作 ABCD,其中C、D在x轴上,则
ABCD,其中C、D在x轴上,则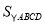 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com