
(10分)如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF= AC.
AC.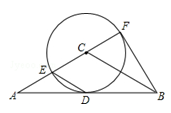
(1)求∠ACB的度数;
(2)若AC=8,求△ABF的面积.
(1)120°;(2)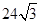 .
.
解析试题分析:(1)连接DC,根据AB是⊙C的切线,所以CD⊥AB,根据CD= AC,得出∠A=30°,因为AC=BC,从而求得∠ACB的度数.
AC,得出∠A=30°,因为AC=BC,从而求得∠ACB的度数.
(2)通过△ACD≌△BCF求得∠AFB=90°,已知AC=8,根据已知求得AF=12,由于∠A=30°得出BF= AB,然后依据勾股定理求得BF的长,即可求得三角形的面积.
AB,然后依据勾股定理求得BF的长,即可求得三角形的面积.
试题解析:(1)连接CD,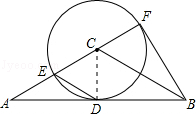
∵AB是⊙C的切线,∴CD⊥AB,∵CF= AC,CF=CE,∴AE=CE,∴ED=
AC,CF=CE,∴AE=CE,∴ED= AC=EC,∴ED=EC=CD,∴∠ECD=60°,∴∠A=30°,∵AC=BC,∴∠ACB=120°;
AC=EC,∴ED=EC=CD,∴∠ECD=60°,∴∠A=30°,∵AC=BC,∴∠ACB=120°;
(2)∵∠A=30°,AC=BC,∴∠ABC=30°,∴∠BCF=60°,在△ACD与△BCF中,∵AC=BC,∠ACD=∠BCF=90°,CD=CF,∴△ACD≌△BCF(SAS),∴∠ADC=∠BFC,∵CD⊥AB,∴CF⊥BF,∵AC=8,CF= AC,∴CF=4,∴AF=12,∵∠AFB=90°,∠A=30°,∴BF=
AC,∴CF=4,∴AF=12,∵∠AFB=90°,∠A=30°,∴BF= AB,设BF=x,则AB=2x,∵
AB,设BF=x,则AB=2x,∵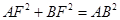 ,∴
,∴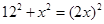 ,解得:
,解得: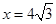 ,即BF=
,即BF=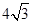 ,∴△ABF的面积=
,∴△ABF的面积= AF·BF=
AF·BF=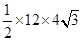 =
=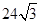 ,
,
考点:切线的性质.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠。点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积。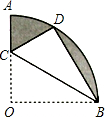
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:解答题
(本题满分10分)已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.

(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:选择题
在一个不透明的口袋中,装有n个除颜色不同其余都相同的球,如果口袋中装有4个红球且摸到红球的概率为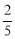 ,那么n等于( )
,那么n等于( )
A.10个 B.12个 C.16个 D.20个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com