【题目】如图，轮船从A港出发，以28海里/小时的速度向正北方向航行，此时测的灯塔M在北偏东30°的方向上．半小时后，轮船到达B处，此时测得灯塔M在北偏东60°的方向上．
（1）求轮船在B处时与灯塔M的距离；
（2）轮船从B处继续沿正北方向航行，又经半小时后到达C处．求：此时轮船与灯塔M的距离是多少？灯塔M在轮船的什么方向上？
【答案】（1）轮船在B处时与灯塔M的距离为14海里；（2）14海里，灯塔M在轮船的南偏东60°方向．
【解析】
（1）根据轮船到达B处，此时测得灯塔M在北偏东60°的方向上，可以得到BA=BM，从而可以得到答案；
（2）计算出BC的长度，根据∠CBM=60°可以判断△ABM为等边三角形，即可求出答案。
解：（1）根据题意可知BA=28×0.5=14海里，
因为此时灯塔M在北偏东60°的方向上，
根据三角形外角定理可以得到∠BAM=∠M
所以BA=BM=14海里，
即轮船在B处时与灯塔M的距离为14海里；
（1）
轮船从B处继续沿正北方向航行，又经半小时后到达C处，
所以BC=28×05=14海里，
所以BC=BM
又因为∠CBM=60°
所以△ABM为等边三角形
所以CM=14海里
所以灯塔M在轮船的南偏东60°方向
科目：初中数学 来源： 题型：
【题目】如图1，在矩形ABCD中，动点E从A出发，沿A→B→C方向运动，当点E到达点C时停止运动，过点E作EF⊥AE交CD于点F，设点E运动路程为x，CF=y，如图2所表示的是y与x的函数关系的大致图象，给出下列结论：①a=3；②当CF=
时，点E的运动路程为
或
或
，则下列判断正确的是（ ）
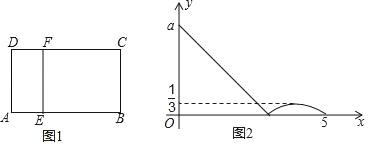
A. ①②都对 B. ①②都错 C. ①对②错 D. ①错②对
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，∠A＝90°，AD∥BC，AB＝4，点P是线段AD上的动点，连接BP，CP，若△BPC周长的最小值为16，则BC的长为（ ）
A.5B.6C.8D.10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，网格图中的每小格均是边长是1的正方形，
与
的顶点均在格点上，请完成下列各题：
（1）在平面直角坐标系中画出与关于x轴对称的
，并写出将沿着x轴向右平移几个单位后得到；
（2）在x轴上求作一点P，使得
的值最大。（要求：保留画图痕迹并直接写出点P的坐标.）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形ABCD的边长是4，点E是AB边上一动点，连接CE，过点B作BG⊥CE于点G，点P是AB边上另一动点，则PD+PG的最小值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CB，垂足为F．
（1）求证：△ABC≌△ADE；
（2）求∠FAE的度数；
（3）求证：CD=2BF+DE．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列解题过程：
=
=
=
-2；
=
=
．
请回答下列问题：
（1）观察上面的解题过程，请直接写出式子
= ；
（2）观察上面的解题过程，请直接写出式子
= ；
（3）利用上面所提供的解法，请求
+···+
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
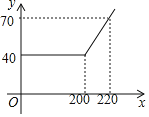
【题目】某网络公司推出了一系列上网包月业务，其中的一项业务是10M“40元包200小时”，且其中每月收取费用y（元）与上网时间x（小时）的函数关系如图所示．
（1）当x≥200时，求y与x之间的函数关系式
（2）若小刚家10月份上网180小时，则他家应付多少元上网费？
（3）若小明家10月份上网费用为52元，则他家该月的上网时间是多少小时？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，△CDE是等边三角形，点D在边AB上．
（1）如图1，当点E在边BC上时，求证DE＝EB；
（2）如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；
（3）如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝3．求CG的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com