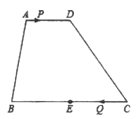
【题目】如图，在四边形
中，
, 
是
的中点.点
以每秒1个单位长度的速度从点
出发，沿
向点
运动;点
同时以每秒3个单位长度的速度从 点
出发，沿
向点
运动.点停止运动时，点也随之停止运动.当运动时间
秒时，以点
为顶点的四边形是平行四边形.则的值为_________.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的探究问题.
（提出问题）三个有理数a，b，c，满足abc>0，求
的值.
（解决问题）
解：由题意得：a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.
①当a，b，c，都是整数，即a>0，b>0，c>0时，则= 
=1+1+1=3；
②当a，b，c有一个为正数，另两个位负数时，设a>0，b<0，c<0，则= 
=111=1；
所以的值为3或1.
（探究）请根据上面的解题思路解答下面的问题：
(1)三个有理数a，b，c满足abc<0，求的值；
(2)已知
=9，
=4，且a<b，求a2b的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
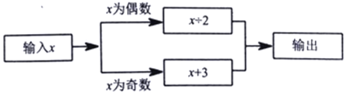
【题目】如图是某运算程序，根据该程序的指令，首先输入
的值为1，则输出的值为4，记作第一次操作；将第一次的输出值再次输入，则输出的值为2，记作第二次操作：…，如此循环操作，则第2020次操作输出的值为________.
查看答案和解析>>
科目：初中数学 来源： 题型：
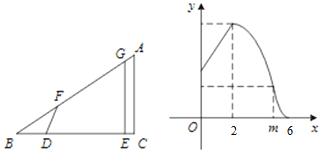
【题目】如图 , 
中， 
，线段
在射线
上，且
，线段
沿射线
运动，开始时，点
与点
重合，点
到达点
时运动停止，过点
作
，与射线
相交于点
，过点
作
的垂线，与射线
相交于点
.设
，四边形
与
重叠部分的面积为
关于
的函数图象如图所示(其中
时，函数的解析式不同)
(1)填空: 
的长是 ;
(2)求
关于
的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
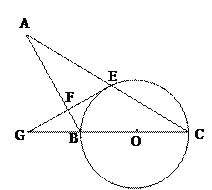
【题目】如图，在△ABC中，以BC为直径的⊙O交AC于点E，过点E作EF⊥AB于点F，延长EF交CB的延长线于点G，且∠ABG=2∠C．
（1）求证：EF是⊙O的切线；
（2）若
，⊙O的半径是3，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对x，y定义一种新运算T，规定：T（x，y）=
（其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）=
=b．
（1）已知T（1，﹣1）=﹣2，T（4，2）=1．
①求a，b的值；
②若关于m的不等式组
恰好有3个整数解，求实数p的取值范围；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则a，b应满足怎样的关系式？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上，点
表示1，现将点沿数轴作如下移动，第一次点向左移动2个单位长度到达点
，第二次将点向右移动4个单位长度到达点
，第三次将点向左移动6个单位长度到达点
，按照这种移动规律移动下去，第
次移动到点
，如果点与原点的距离是21，那么的值是________________．
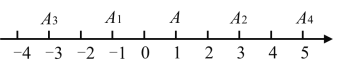
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AE是∠BAC的角平分线，交BC于点E，DE∥AB交AC于点D．
(1)求证AD=ED；
(2)若AC=AB，DE=3，求AC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
