
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的探究问题.
(提出问题)三个有理数a,b,c,满足abc>0,求![]() 的值.
的值.
(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c,都是整数,即a>0,b>0,c>0时,则![]() =
= ![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个位负数时,设a>0,b<0,c<0,则![]() =
= ![]() =111=1;
=111=1;
所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(2)已知![]() =9,
=9,![]() =4,且a<b,求a2b的值.
=4,且a<b,求a2b的值.
【答案】(1)-3或1;(2)17或1.
【解析】
(1)按照题目内的求值方式,分类讨论,即可解答.
(2)根据![]() =9,
=9,![]() =4分别求出a、b的值,再根据a<b,分情况讨论,分别求出a2b的值即可.
=4分别求出a、b的值,再根据a<b,分情况讨论,分别求出a2b的值即可.
(1)∵abc<0,
∴a,b,c都是负数或其中一个为负数,另两个为正数,
①当a,b,c都是负数,即a<0,b<0,c<0时,则原式=111=3;
②a,b,c有一个为负数,另两个为正数时,不妨设a<0,b>0,c>0,则原式=1+1+1=1;
(2) ∵ ![]() =9,
=9,![]() =4
=4
∴a=![]() 9,b=±4
9,b=±4
∵a<b,
∴当a=-9,b=4时,a2b=92×4=-17,
当a=-9,b=-4时,a2b=92×(-4)=-1,


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,O是AB的中点,连接DO并延长交CB的延长线于点E,连接AE、DB.
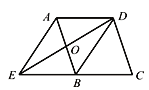
(1)求证:△AOD≌△BOE;
(2)若DC=DE,判断四边形AEBD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
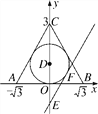
【题目】(2016·衡阳中考)如图,在平面直角坐标系中,△ABC三个顶点坐标为A(-![]() ,0),B(
,0),B(![]() ,0),C(0,3).
,0),C(0,3).
(1)求△ABC内切圆⊙D的半径;
(2)过点E(0,-1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB连接EF,证明:△AED≌△AEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用抽样调查方式的是( )
A.调查某航空公司飞行员视力的达标率
B.调查乘坐飞机的旅客是否携带了违禁物品
C.调查某品牌圆珠笔芯的使用寿命
D.调查你组6名同学对太原市境总面积的知晓情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节来临之际,学校准备购进一批树苗,已知2棵甲种树苗和5棵乙种树苗共需113元;3棵甲种树苗和2棵乙种树苗共需87元.
(1)求一棵甲种树苗和一棵乙种树苗的售价各是多少元?
(2)学校准备购进这两种树苗共100棵,并且乙种树苗的数量不多于甲种树苗数量的2倍,请设计出最省钱的购买方案,并求出此时的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
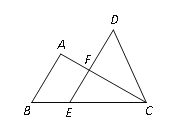
【题目】如图为△ABC与△DEC重叠的情形,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=2,AB=3,则DF的长等于_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
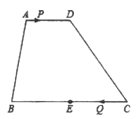
【题目】如图,在四边形![]() 中,
中,![]() ,
, ![]() 是
是![]() 的中点.点
的中点.点![]() 以每秒1个单位长度的速度从点
以每秒1个单位长度的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动;点
运动;点![]() 同时以每秒3个单位长度的速度从 点
同时以每秒3个单位长度的速度从 点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.点
运动.点![]() 停止运动时,点
停止运动时,点![]() 也随之停止运动.当运动时间
也随之停止运动.当运动时间![]() 秒时,以点
秒时,以点![]() 为顶点的四边形是平行四边形.则
为顶点的四边形是平行四边形.则![]() 的值为_________.
的值为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com