
【题目】如图,在平行四边形ABCD中,O是AB的中点,连接DO并延长交CB的延长线于点E,连接AE、DB.
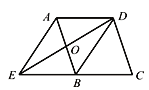
(1)求证:△AOD≌△BOE;
(2)若DC=DE,判断四边形AEBD的形状,并说明理由.
【答案】(1)证明见解析;(2)四边形AEBD是矩形.
【解析】
(1)利用平行线得到∠ADO=∠BEO,再利用对顶角相等和线段中点,可证明△AOD≌△BOE;
(2)先证明四边形AEBD是平行四边形,再利用对角线相等的平行四边形的矩形,可判定四边形AEBD是矩形.
(1)∵四边形ABCD是平行四边形,∴AD∥CE,∴∠ADO=∠BEO.
∵O是BC中点,∴AO=BO.
又∵∠AOD=∠BOE,∴△AOD≌△BOE(AAS);
(2)四边形AEBD是矩形,理由如下:
∵△AOD≌△BOE,∴DO=EO.
又AO=BO,∴四边形AEBD是平行四边形.
∵DC=DE=AB,∴四边形AEBD是矩形.


科目:初中数学 来源: 题型:
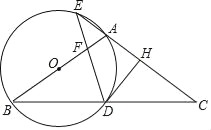
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中![]() ,n=-1.”小强不小心把
,n=-1.”小强不小心把![]() 错抄成了
错抄成了![]() ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
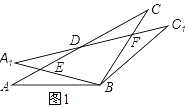
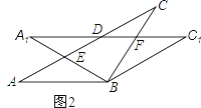
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B两点,且AB=8,点A表示的数为6;动点P从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)写出数轴上点B表示的数是 ;
(2)当t=2时,线段PQ的长是 ;
(3)当0<t<3时,则线段AP= ;(用含t的式子表示)
(4)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
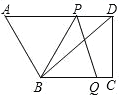
【题目】如图,在四边形ABCD中,AD//BC, ![]() ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 与
与![]() 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时![]() 的值.
的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出![]() =_____________.
=_____________.
(4)是否存在时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城相距1000千米,一辆客车从甲城开往乙城,车速为![]() 千米/小时,同时一辆出租车从乙城开往甲城,车速为90千米/小时,设客车行驶时间为
千米/小时,同时一辆出租车从乙城开往甲城,车速为90千米/小时,设客车行驶时间为![]() (小时)
(小时)
(1)当![]() 时,客车与乙城的距离为 千米(用含
时,客车与乙城的距离为 千米(用含![]() 的代数式表示)
的代数式表示)
(2)已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米
①求客车与出租车相距100千米时客车的行驶时间;(列方程解答)
②已知客车与出租车在甲、乙之间的服务站![]() 处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在![]() 处换成客车返回乙城.
处换成客车返回乙城.
是通过计算,分析小王选择哪种方案能更快到达乙城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的探究问题.
(提出问题)三个有理数a,b,c,满足abc>0,求![]() 的值.
的值.
(解决问题)
解:由题意得:a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c,都是整数,即a>0,b>0,c>0时,则![]() =
= ![]() =1+1+1=3;
=1+1+1=3;
②当a,b,c有一个为正数,另两个位负数时,设a>0,b<0,c<0,则![]() =
= ![]() =111=1;
=111=1;
所以![]() 的值为3或1.
的值为3或1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足abc<0,求![]() 的值;
的值;
(2)已知![]() =9,
=9,![]() =4,且a<b,求a2b的值.
=4,且a<b,求a2b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com