
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
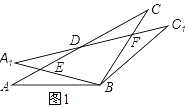
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
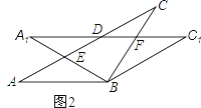
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
【答案】(1)BE=DF;(2)四边形BC1DA是菱形.
【解析】
(1)由AB=BC得到∠A=∠C,再根据旋转的性质得AB=BC=BC1,∠A=∠C=∠C1,∠ABE=∠C1BF,则可证明△ABE≌△C1BF,于是得到BE=BF
(2)根据等腰三角形的性质得∠A=∠C=30°,利用旋转的性质得∠A1=∠C1=30°,∠ABA1=∠CBC1=30°,则利用平行线的判定方法得到A1C1∥AB,AC∥BC1,于是可判断四边形BC1DA是平行四边形,然后加上AB=BC1可判断四边形BC1DA是菱形.
(1)解:BE=DF.理由如下:
∵AB=BC,
∴∠A=∠C,
∵△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,
∴AB=BC=BC1,∠A=∠C=∠C1,∠ABE=∠C1BF,
在△ABE和△C1BF中
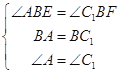 ,
,
∴△ABE≌△C1BF,
∴BE=BF
(2)解:四边形BC1DA是菱形.理由如下:
∵AB=BC=2,∠ABC=120°,
∴∠A=∠C=30°,
∴∠A1=∠C1=30°,
∵∠ABA1=∠CBC1=30°,
∴∠ABA1=∠A1,∠CBC1=∠C,
∴A1C1∥AB,AC∥BC1,
∴四边形BC1DA是平行四边形.
又∵AB=BC1,
∴四边形BC1DA是菱形


科目:初中数学 来源: 题型:
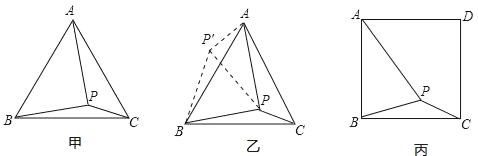
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
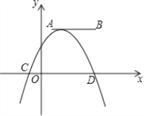
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解题过程.
已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.若∠AOC=60°,求∠DOE数.
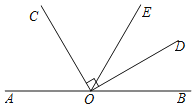
解:∵O是直线AB上的一点,(已知)
∴∠BOC=180°﹣∠AOC.(_________)
∵∠AOC=60°,(已知)
∴∠BOC=120°.(_________)
∵OE平分∠BOC,(已知)
∴∠COE=![]() ∠BOC,(_________)
∠BOC,(_________)
∴∠COE=_____°.
∵∠DOE=∠COD﹣∠COE,且∠COD=90°,
∴∠DOE=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,O是AB的中点,连接DO并延长交CB的延长线于点E,连接AE、DB.
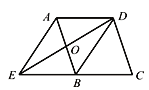
(1)求证:△AOD≌△BOE;
(2)若DC=DE,判断四边形AEBD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
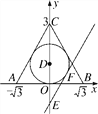
【题目】(2016·衡阳中考)如图,在平面直角坐标系中,△ABC三个顶点坐标为A(-![]() ,0),B(
,0),B(![]() ,0),C(0,3).
,0),C(0,3).
(1)求△ABC内切圆⊙D的半径;
(2)过点E(0,-1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
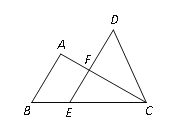
【题目】如图为△ABC与△DEC重叠的情形,其中E在BC上,AC交DE于F点,且AB∥DE.若△ABC与△DEC的面积相等,且EF=2,AB=3,则DF的长等于_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com