
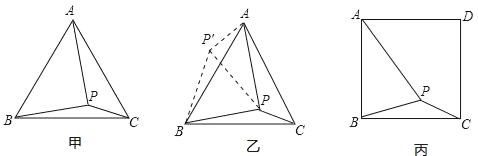
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
【答案】(1)等边 直角 150°;(2)![]() ;(3)135°;(4)
;(3)135°;(4)![]() .
.
【解析】
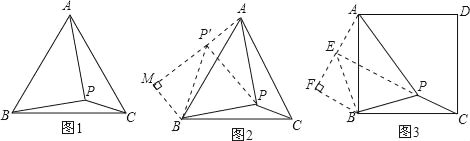
(1)将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,
(2)过点B作BM⊥AP′,交AP′的延长线于点M,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
(3)求出![]() ,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
(4)过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
解:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
将△BPC绕点B顺时针旋转60°得出△ABP′,
∴![]()
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴![]()
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,则△PP′A是 直角三角形;
∴∠BPC=∠AP′B=90°+60°=150°;
(2)过点B作BM⊥AP′,交AP′的延长线于点M,
∴![]()
由勾股定理得: ![]()
∴![]()
由勾股定理得: ![]()
故答案为:(1)等边;直角;150;![]() ;
;
(3)将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=![]() ,∠BPC=∠AEB,∠ABE=∠PBC,
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴![]() ,
,
由勾股定理得:EP=2,
∵![]()
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°;
(4)过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.
答:(3)∠BPC的度数是135°;
(4)正方形ABCD的边长是![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】某股民上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元)(周六、周日休盘)
星期 | 一 | 二 | 三 | 四 | 五 |
每股 涨跌 | +4 | +4.5 | -1 | -1.5 | -4 |
(1)星期五收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知该股民买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,若该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
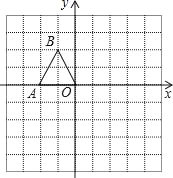
【题目】如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1,与△OAB对应线段的比为2:1,画出△OA1B1,(所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标_____;
(3)直接写出tan∠OA1B1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,把
,读作“2的圈3次方”,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈4次方”,一般地,把
的圈4次方”,一般地,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,关于除方,下列说法错误的是( )
次方”,关于除方,下列说法错误的是( )
A.任何非零数的圈2次方都等于1
B.对于任何正整数![]() ,
,![]()
C.![]()
D.负数的圈奇次方结果是负数,负数的圈偶次方结果是正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中![]() ,n=-1.”小强不小心把
,n=-1.”小强不小心把![]() 错抄成了
错抄成了![]() ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
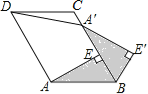
A. 130° B. 150° C. 160° D. 170°
查看答案和解析>>
科目:初中数学 来源: 题型:
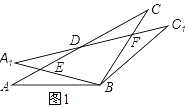
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
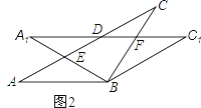
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
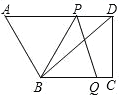
【题目】如图,在四边形ABCD中,AD//BC, ![]() ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 与
与![]() 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时![]() 的值.
的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出![]() =_____________.
=_____________.
(4)是否存在时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.

根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com