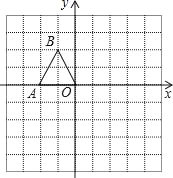
【题目】如图，在边长均为1的小正方形网格纸中，△OAB的顶点O，A，B均在格点上，且O是直角坐标系的原点，点A在x轴上．
（1）以O为位似中心，将△OAB放大，使得放大后的△OA1B1，与△OAB对应线段的比为2：1，画出△OA1B1，（所画△OA1B1与△OAB在原点两侧）；
（2）直接写出点A1、B1的坐标_____；
（3）直接写出tan∠OA1B1．
科目：初中数学 来源： 题型：
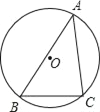
【题目】如图，锐角△ABC内接于⊙O，若⊙O的半径为6，sinA=
，求BC的长．
【答案】BC=8．
【解析】试题分析：通过作辅助线构成直角三角形，再利用三角函数知识进行求解．
试题解析：作⊙O的直径CD，连接BD，则CD=2×6=12.
∵
∴
∴
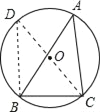
点睛：直径所对的圆周角是直角.
【题型】解答题
【结束】
22
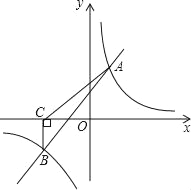
【题目】如图，一次函数y=k1x+b与反比例函数y=
的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S△ABC=5．
（1）求一次函数与反比例函数的解析式；
（2）根据所给条件，请直接写出不等式k1x+b＞的解集；
（3）若P（p，y1），Q（﹣2，y2）是函数y=图象上的两点，且y1≥y2，求实数p的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
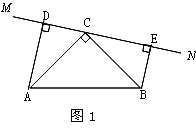
【题目】如图，在△ABC中，
，
，直线
经过点
，且
于
，
于
.
(1)当直线绕点旋转到图1的位置时，
①求证：△ADC≌△CEB.
②求证：DE=AD+BE.
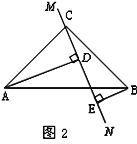
(2)当直线绕点旋转到图2的位置时，判断
和
的关系，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【操作发现】
如图①，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上．
（1）请按要求画图：将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B′，点C的对应点为C′，连接BB′；
（2）在（1）所画图形中，∠AB′B= ．
【问题解决】
如图②，在等边三角形ABC中，AC=7，点P在△ABC内，且∠APC=90°，∠BPC=120°，求△APC的面积．
小明同学通过观察、分析、思考，对上述问题形成了如下想法：
想法一：将△APC绕点A按顺时针方向旋转60°，得到△AP′B，连接PP′，寻找PA，PB，PC三条线段之间的数量关系；
想法二：将△APB绕点A按逆时针方向旋转60°，得到△AP′C′，连接PP′，寻找PA，PB，PC三条线段之间的数量关系．
…
请参考小明同学的想法，完成该问题的解答过程．（一种方法即可）
【灵活运用】
如图③，在四边形ABCD中，AE⊥BC，垂足为E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k为常数），求BD的长（用含k的式子表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
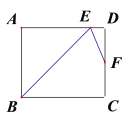
【题目】如图，在矩形ABCD中，∠B的平分线BE与AD交于点E，∠BED的平分线EF与DC交于点F，当点F是CD的中点时，若AB=4，则BC=_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
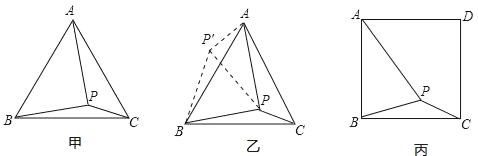
【题目】如图甲，在等边三角形ABC内有一点P，且PA＝2，PB＝
，PC＝1，求∠BPC度数的大小和等边三角形ABC的边长．
解题思路是：将△BPC绕点B逆时针旋转60°，如图乙所示，连接PP′．
（1）△P′PB是 三角形，△PP′A是 三角形，∠BPC＝ °；
（2）利用△BPC可以求出△ABC的边长为 ．
如图丙，在正方形ABCD内有一点P，且PA＝
，BP＝
，PC＝1；
（3）求∠BPC度数的大小；
（4）求正方形ABCD的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
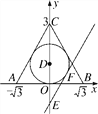
【题目】(2016·衡阳中考)如图，在平面直角坐标系中，△ABC三个顶点坐标为A(－
，0)，B(
，0)，C(0，3)．
(1)求△ABC内切圆⊙D的半径；
(2)过点E(0，－1)的直线与⊙D相切于点F(点F在第一象限)，求直线EF的解析式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
