
【题目】如图,在△ABC中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)当直线![]() 绕点
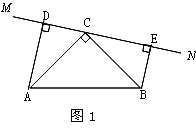
绕点![]() 旋转到图1的位置时,
旋转到图1的位置时,
①求证:△ADC≌△CEB.
②求证:DE=AD+BE.
(2)当直线![]() 绕点
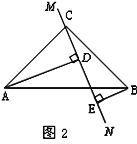
绕点![]() 旋转到图2的位置时,判断
旋转到图2的位置时,判断![]() 和
和![]() 的关系,并说明理由.
的关系,并说明理由.
【答案】(1)①见解析;②见解析;(2)△ADC≌△CEB;理由见解析
【解析】
(1)①要证△ADC≌△CEB,已知一直角∠ADC=∠CEB=90°和一边AC=CB对应相等,由题意根据同角的余角相等,可得另一内角∠ECB=∠DAC,再由AAS即可判定;
②由①得出AD=CE,BE=CD,而DE=CD+CE,故DE=AD+BE;
(2)同理,根据上一小题的解题思路,易得△ADC≌△CEB.
(1)①∵∠ACB=90°
∴∠DCA+∠ECB=90°
又∵AD⊥MN
∴∠DCA+∠DAC=90°
∴∠ECB=∠DAC
又∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
在△ADC和△CEB中
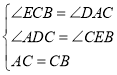
∴△ADC≌△CEB(AAS)
②∵△ADC≌△CEB
∴AD=CE,BE=CD
又∵DE=CD+CE
∴DE=AD+BE
(2)△ADC≌△CEB;
∵∠ACB=90°
∴∠DCA+∠ECB=90°
又∵AD⊥MN
∴∠DCA+∠DAC=90°
∴∠ECB=∠DAC
又∵AD⊥MN,BE⊥MN
∴∠ADC=∠CEB=90°
在△ADC和△CEB中
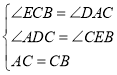
∴△ADC≌△CEB(AAS)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
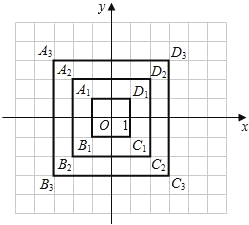
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股民上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况(单位:元)(周六、周日休盘)
星期 | 一 | 二 | 三 | 四 | 五 |
每股 涨跌 | +4 | +4.5 | -1 | -1.5 | -4 |
(1)星期五收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知该股民买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,若该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点![]() ,
,![]() ,
,![]() ,把
,把![]() 向下平移
向下平移![]() 个单位再向右平移
个单位再向右平移![]() 个单位后得
个单位后得![]() .
.

(1)画出平移后的图形,直接写出![]() ,
,![]() ,
,![]() 三个对应点
三个对应点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)求![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
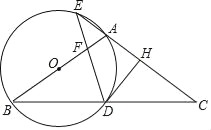
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点 A、B 在数轴上分别表示有理数 a、b,A、B 两点之间的距离表示为 AB, 在数轴上 A、B 两点之间的距离 AB=|a﹣b|.
![]()
请用上面的知识解答下面的问题:
(1)数轴上表示 1 和 5 的两点之间的距离是 ,数轴上表示﹣2 和﹣4 的 两点之间的距离是 ,数轴上表示 1 和﹣3 的两点之间的距离是 ;
(2)数轴上表示 x 和﹣1 的两点 A 和 B 之间的距离是 ,如果|AB|=2, 那么 x 为 ;
(3)|x+1|+|x﹣2|取最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
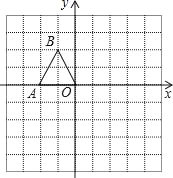
【题目】如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在x轴上.
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1,与△OAB对应线段的比为2:1,画出△OA1B1,(所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标_____;
(3)直接写出tan∠OA1B1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如![]() ,
,![]() 等,类比有理数的乘方,我们把
等,类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“2的圈3次方”,把
,读作“2的圈3次方”,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈4次方”,一般地,把
的圈4次方”,一般地,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,关于除方,下列说法错误的是( )
次方”,关于除方,下列说法错误的是( )
A.任何非零数的圈2次方都等于1
B.对于任何正整数![]() ,
,![]()
C.![]()
D.负数的圈奇次方结果是负数,负数的圈偶次方结果是正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
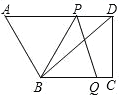
【题目】如图,在四边形ABCD中,AD//BC, ![]() ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 与
与![]() 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时![]() 的值.
的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出![]() =_____________.
=_____________.
(4)是否存在时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com