
����Ŀ��ij���������������ij��˾��Ʊ1000�ɣ�ÿ��27Ԫ���±�Ϊ������ÿ�ոù�Ʊ���ǵ��������λ��Ԫ�����������������̣�
���� | һ | �� | �� | �� | �� |
ÿ�� �ǵ� | +4 | +4.5 | ��1 | ��1.5 | ��4 |
��1������������ʱ��ÿ���Ƕ���Ԫ��
��2�������������ÿ�ɶ���Ԫ����ͼ���ÿ�ɶ���Ԫ��
��3����֪�ù��������Ʊʱ����0.15%�������ѣ�����ʱ�踶�ɽ���0.15%�������Ѻ�0.1%�Ľ���˰�����ù���������������ǰ��ȫ����Ʊ�������������������Σ�
���𰸡���1��29Ԫ��2�����35.5Ԫ����ͼ�29Ԫ��3��![]() Ԫ
Ԫ
��������
��1�����ñ�������ֱ�ӽ����������ļӼ����㣻��2�����ñ�������ֱ�ӽ����������ļӼ����㣻��3������=������Ʊ��-�����Ʊ��-���������-��������˰���㼴�ɣ�
��1����������ã���������ʱ��ÿ�ɼ۸�Ϊ��27+4+4.5-1-1.5-4=29��Ԫ����
��2��������֪����ã���һ�ǣ��ܶ��ǣ����������ġ����������
�౾��������ܶ�����ͼ������壻
�����=27+4+4.5=35.5��Ԫ������ͼ�=27+4+4.5-1-1.5-4=29��Ԫ����
��3��������ã�
����������ѣ�![]() ��Ԫ����
��Ԫ����
�����Ľ���˰��![]() ��Ԫ����
��Ԫ����
����=������Ʊ��-�����Ʊ��-���������-��������˰��
������Ϊ��![]() =1887��Ԫ��.
=1887��Ԫ��.
����������ʱÿ�ɼ۸�Ϊ29Ԫ�����ܵ������ÿ��35.5Ԫ����ͼ���ÿ��29Ԫ��������������ǰ�������ù�������Ϊ1887Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
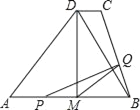
����Ŀ����ͼ��MΪ������ABD�ĵ�AB���е㣬��D��DC��AB������BC��AB=8cm��DM=4cm��DC=1cm������P��A���������AB�������˶�������Q�Ե�B������������BC��CD�������˶����ٶȾ�Ϊ1cm/s��������һ�����㵽���յ�ʱ������ͬʱֹͣ�˶������P�˶�t��s��ʱ����MPQ�����ΪS�����ܹ��ɡ�MPQ�Ķ�����⣩��
��1��t��s��Ϊ��ֵʱ����Q��BC���˶���t��s��Ϊ��ֵʱ����Q��CD���˶���
��2����S��t֮��ĺ�����ϵʽ��
��3����tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��4������Q��CD���˶�ʱ��ֱ��д��tΪ��ֵʱ����MPQ�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABC�ڽ�����O������O�İ뾶Ϊ6��sinA=![]() ����BC�ij���
����BC�ij���
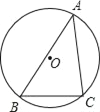
���𰸡�BC=8��
�����������������ͨ���������߹���ֱ�������Σ����������Ǻ���֪ʶ������⣮
�������������O��ֱ��CD������BD����CD=2��6=12.
��![]()
��![]()
��![]()
�㾦��ֱ�����Ե�Բ�ܽ���ֱ��.
�����͡������
��������
22
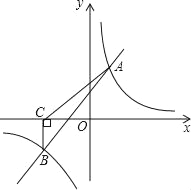
����Ŀ����ͼ��һ�κ���y=k1x+b�뷴��������y=![]() ��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��ͼ����A��2��m����B��n����2�����㣮����B��BC��x�ᣬ����ΪC����S��ABC=5��
��1����һ�κ����뷴���������Ľ���ʽ��
��2������������������ֱ��д������ʽk1x+b��![]() �Ľ⼯��
�Ľ⼯��
��3����P��p��y1����Q����2��y2���Ǻ���y=![]() ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��
ͼ���ϵ����㣬��y1��y2����ʵ��p��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ����ƽ��ֱ������ϵ�У���
����ƽ��ֱ������ϵ�У���![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() �����߶�
�����߶�![]() ������ƽ��
������ƽ��![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ��![]() ����λ���ȣ��õ��߶�
����λ���ȣ��õ��߶�![]() ������
������![]() ��
��![]() ������ƽ���ı���
������ƽ���ı���![]() ��
��
��1����д����![]() ������Ϊ________����
������Ϊ________����![]() ������Ϊ________��
������Ϊ________��![]() ________��
________��
��2����![]() ��
��![]() ���ϣ���
���ϣ���![]() �������
�������![]() �����ꣻ
�����ꣻ
��3����ͼ![]() ����
����![]() ���߶�
���߶�![]() ������һ���㣨����
������һ���㣨����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ����̽��
����̽��![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ����֤����Ľ��ۣ�
֮��Ĺ�ϵ����֤����Ľ��ۣ�
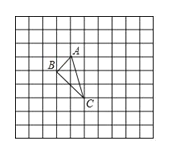
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
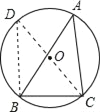
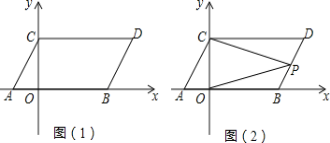
����Ŀ����ͼ�������������е���ABC����С����߳�Ϊ1�������ABC�������������߽���������Σ��Ķ���A��C������ֱ�Ϊ����1��1������0����2�������������ѧ��֪ʶ��
��1������ͼ��ʾ������ƽ��������ƽ��ֱ������ϵ��
��2��������ABC����y��ԳƵ�������A1B1C1��
��3���ж���ABC����״���������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ڱ�ֱ�ĵ�·![]() ��������У��������г���
��������У��������г���![]() �ص�
�ص�![]() �أ��Ҽݳ���
�أ��Ҽݳ���![]() �ص�
�ص�![]() �أ��������Ƿֱ��Բ�ͬ���ٶ�������ʻ�����ȳ�6���Ӻ��Ҳų������ҵ��ٶ�Ϊ
�أ��������Ƿֱ��Բ�ͬ���ٶ�������ʻ�����ȳ�6���Ӻ��Ҳų������ҵ��ٶ�Ϊ![]() ǧ��/�֣������������У��ס�������֮��ľ���
ǧ��/�֣������������У��ס�������֮��ľ���![]() ��ǧ�ף���׳�����ʱ��
��ǧ�ף���׳�����ʱ��![]() ���֣�֮��IJ��ֺ���ͼ����ͼ��
���֣�֮��IJ��ֺ���ͼ����ͼ��
��1��![]() �������______ǧ�ף����ٶ�Ϊ______ǧ��/�֣�
�������______ǧ�ף����ٶ�Ϊ______ǧ��/�֣�
��2��ֱ��д����![]() ������______�����߶�
������______�����߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��3�����ҵ����յ�![]() ʱ������______���ӵ����յ�
ʱ������______���ӵ����յ�![]() ��
��
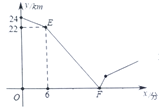
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У�![]() ����AD=12cm,��BC�ij�Ϊ�� ��
����AD=12cm,��BC�ij��� ��
A. 14 cm B. 4 cm C. 14cm��4 cm D. ���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
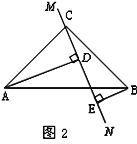
����Ŀ����ͼ���ڡ�ABC�У�![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() .
.
(1)��ֱ��![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ1��λ��ʱ��
��ת��ͼ1��λ��ʱ��
����֤����ADC�ա�CEB.
����֤��DE=AD+BE.
(2)��ֱ��![]() �Ƶ�
�Ƶ�![]() ��ת��ͼ2��λ��ʱ���ж�
��ת��ͼ2��λ��ʱ���ж�![]() ��
��![]() �Ĺ�ϵ����˵������.
�Ĺ�ϵ����˵������.
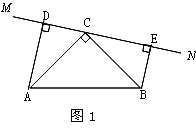
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
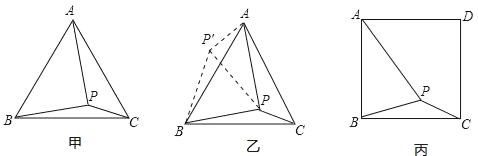
����Ŀ����ͼ�ף��ڵȱ�������ABC����һ��P����PA��2��PB��![]() ��PC��1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
��PC��1�����BPC�����Ĵ�С�͵ȱ�������ABC�ı߳���
����˼·�ǣ�����BPC�Ƶ�B��ʱ����ת60�㣬��ͼ����ʾ������PP�䣮
��1����P��PB�� �����Σ���PP��A�� �����Σ���BPC�� �㣻
��2�����á�BPC���������ABC�ı߳�Ϊ ��
��ͼ������������ABCD����һ��P����PA��![]() ��BP��
��BP��![]() ��PC��1��
��PC��1��
��3�����BPC�����Ĵ�С��
��4����������ABCD�ı߳���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com