
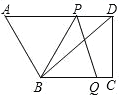
【题目】如图,在四边形ABCD中,AD//BC, ![]() ,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
,BC=4,DC=3,AD=6.动点P从点D出发,沿射线DA的方向,在射线DA上以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P、Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 与
与![]() 之间的函数关系式是____________(不写取值范围).
之间的函数关系式是____________(不写取值范围).
(2)当B,P,Q三点为顶点的三角形是等腰三角形时,求出此时![]() 的值.
的值.
(3)当线段PQ与线段AB相交于点O,且2OA=OB时,直接写出![]() =_____________.
=_____________.
(4)是否存在时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
, ![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】试题分析:
(1)由题意可得BQ=BC-CQ=4-t,点P到BC的距离=CD=3,由此结合三角形的面积公式即可得到S与t之间的函数关系式;
(2)过点P作PH⊥BC于点H,结合勾股定理和已知条件把BP2、BQ2、PQ2用含“t”的代数式表达出来,然后分BP=BQ、BP=PQ、BQ=PQ三种情况列出方程,解方程得到对应的t的值,再结合题中的条件检验即可得到符合要求的t的值;
(3)如图2,过点P作PM⊥BC交CB的延长线于点M,易证得四边形PMCD是矩形,由此可得PM=CD=3,CM=PD=2t,结合AD=6,BC=4,可得PA=2t-6,BQ=4-t,MQ=CM-CQ=t,由AD∥BC可得△OAP∽△OBQ,结合2OA=OB即可求得t的值,从而可由tan∠BQP=![]() 求得其值;
求得其值;
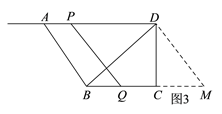
(4)如图3,过点D作DM∥PQ交BC的延长线于点M,则当∠BDM=90°时,PQ⊥BD,即当BM2=DM2+BD2时,PQ⊥BD,由此结合已知条件把DM2、BM2和BD2用含“t”的式子表达出来,列出方程就可得解得t的值.
试题解析:
(1)由题意可得BQ=BC-CQ=4-t,点P到BC的距离=CD=3,
∴S△PBQ=![]() BQ×3=
BQ×3=![]() ;
;
(2)如下图,过点P作PH⊥BC于点H,
∴∠PHB=∠PHQ=90°,
∵∠C=90°,AD∥BC,
∴∠CDP=90°,
∴四边形PHCD是矩形,
∴PH=CD=3,HC=PD=2t,
∵CQ=t,BC=4,
∴HQ=CH-CQ=t,BH=BC-CH=4-2t,BQ=4-t,
∴BQ2=![]() ,BP2=
,BP2=![]() ,PQ2=
,PQ2=![]() ,
,
由BQ2=BP2可得: ![]() ,解得:无解;
,解得:无解;
由BQ2=PQ2可得: ![]() ,解得:
,解得: ![]() ;
;
由BP2= PQ2可得: ![]()
![]() ,解得:
,解得: ![]() 或
或![]() ,
,
∵当![]() 时,BQ=4-4=0,不符合题意,
时,BQ=4-4=0,不符合题意,
∴综上所述, ![]() 或
或![]() ;
;
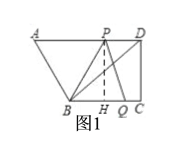
(3)如图2,过点P作PM⊥BC交CB的延长线于点M,
∴∠PMC=∠C=90°,
∵AD∥BC,
∴∠D=90°,△OAP∽△OBQ,
∴四边形PMCD是矩形, ![]() ,
,
∴PM=CD=3,CM=PD=2t,
∵AD=6,BC=4,CQ=t,
∴PA=2t-6,BQ=4-t,MQ=CM-CQ=2t-t=t,
∴![]() ,解得:
,解得: ![]() ,
,
∴MQ= ![]() ,
,
又∵PM=3,∠PMQ=90°,
∴tan∠BPQ=![]() ;
;
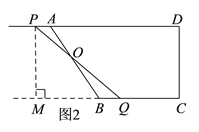
(4)如图3,过点D作DM∥PQ交BC的延长线于点M,则当∠BDM=90°时,PQ⊥BD,即当BM2=DM2+BD2时,PQ⊥BD,
∵AD∥BC,DM∥PQ,
∴四边形PQMD是平行四边形,
∴QM=PD=2t,
∵QC=t,
∴CM=QM-QC=t,
∵∠BCD=∠MCD=90°,
∴BD2=BC2+DC2=25,DM2=DC2+CM2=9+t2,
∵BM2=(BC+CM)2=(4+t)2,
∴由BM2=BD2+DM2可得: ![]() ,解得:
,解得: ![]() ,
,
∴当![]() 时,∠BDM=90°,
时,∠BDM=90°,
即当![]() 时,PQ⊥BD.
时,PQ⊥BD.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
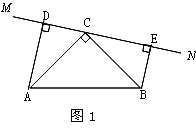
【题目】如图,在△ABC中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,且
,且![]() 于
于![]() ,
,![]() 于
于![]() .
.
(1)当直线![]() 绕点
绕点![]() 旋转到图1的位置时,
旋转到图1的位置时,
①求证:△ADC≌△CEB.
②求证:DE=AD+BE.
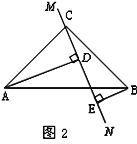
(2)当直线![]() 绕点
绕点![]() 旋转到图2的位置时,判断
旋转到图2的位置时,判断![]() 和
和![]() 的关系,并说明理由.
的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
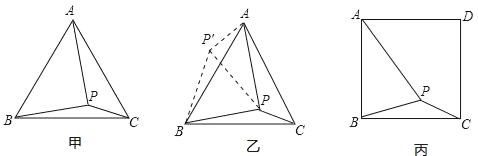
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解题过程.
已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.若∠AOC=60°,求∠DOE数.
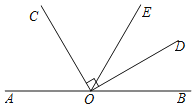
解:∵O是直线AB上的一点,(已知)
∴∠BOC=180°﹣∠AOC.(_________)
∵∠AOC=60°,(已知)
∴∠BOC=120°.(_________)
∵OE平分∠BOC,(已知)
∴∠COE=![]() ∠BOC,(_________)
∠BOC,(_________)
∴∠COE=_____°.
∵∠DOE=∠COD﹣∠COE,且∠COD=90°,
∴∠DOE=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,O是AB的中点,连接DO并延长交CB的延长线于点E,连接AE、DB.
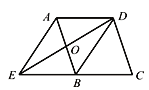
(1)求证:△AOD≌△BOE;
(2)若DC=DE,判断四边形AEBD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
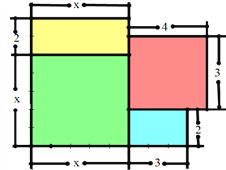
【题目】李叔叔在“中央山水”买了一套经济适用房,他准备将地面铺上地砖,这套住宅的建筑平面(由四个长方形组成)如图所示(图中长度单位:米),请解答下问题:
(1)用式子表示这所住宅的总面积;
(2)若铺1平方米地砖平均费用120元,求当x=6时,这套住宅铺地砖总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
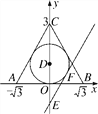
【题目】(2016·衡阳中考)如图,在平面直角坐标系中,△ABC三个顶点坐标为A(-![]() ,0),B(
,0),B(![]() ,0),C(0,3).
,0),C(0,3).
(1)求△ABC内切圆⊙D的半径;
(2)过点E(0,-1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用抽样调查方式的是( )
A.调查某航空公司飞行员视力的达标率
B.调查乘坐飞机的旅客是否携带了违禁物品
C.调查某品牌圆珠笔芯的使用寿命
D.调查你组6名同学对太原市境总面积的知晓情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com