
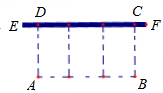
 23、如图,EF是一面长18米的墙,用总长为32米的木栅栏(图中的虚线)围一个矩形场地,中间还要隔成三块.设与墙头垂直的边AD长为x米,
23、如图,EF是一面长18米的墙,用总长为32米的木栅栏(图中的虚线)围一个矩形场地,中间还要隔成三块.设与墙头垂直的边AD长为x米, 解:(1)∵与墙头垂直的边AD长为x米,四边形ABCD是矩形,
解:(1)∵与墙头垂直的边AD长为x米,四边形ABCD是矩形,

科目:初中数学 来源: 题型:
 用长为12米的篱笆,围成如图所示的矩形兔场ABCD,其中一面是长为8米的墙,中间EF是篱笆隔离栏.
用长为12米的篱笆,围成如图所示的矩形兔场ABCD,其中一面是长为8米的墙,中间EF是篱笆隔离栏.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
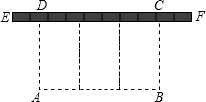 垂直的边AD长为x米,
垂直的边AD长为x米,查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川省遂宁市安居中学九年级(上)期末复习数学试卷(解析版) 题型:解答题
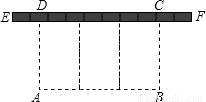
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北省武汉市光谷实验中学九年级(上)月考数学试卷(9月份)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com