【题目】已知：如图，在△ABC中，CB=CA，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

（1）判断DE与⊙O的位置关系，并证明你的结论；

（2）若BD=1，cosB=，求的长．

参考答案：

【答案】（1）DE是⊙O的切线；证明见解析；（2）．

【解析】

试题分析：（1）根据圆周角定理证得CD⊥AB，根据等腰三角形三线合一的性质得出AD=BD，根据三角形中位线定理得出OD∥AC，证得DE⊥DO，即可证得结论；

（2）证得△OBD是等边三角形，求得圆心角和半径，根据弧长公式即可求得．

试题解析：（1）连接CD，

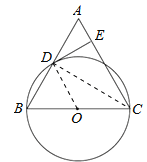
∵BC是圆的直径，

∴∠BDC=90°，

∴CD⊥AB，

又∵AC=BC，

∴AD=BD，

连接OD，则DO是△ABC的中位线，

∴DO∥AC，

又∵DE⊥AC，

∴DE⊥DO，

∴DE是⊙O的切线；

（2）∵cosB=，

∴∠B=60°，

∵OB=OD，

∴△OBD是等边三角形，

∴∠BOD=60°，OB=OD=BD=1，

∴的长=．

关闭