
【题目】已知,![]() 内接于
内接于![]() ,点
,点![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 、
、![]() ;
;
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.

【答案】(1)见解析;(2)见解析;(3)2![]() .
.
【解析】
(1)由点P是弧AB的中点,可得出AP=BP, 通过证明![]() ,
,![]() 可得出
可得出![]() 进而证明AB
进而证明AB![]() PC.
PC.
(2)由PA是∠CPM的角平分线,得到∠MPA=∠APC, 等量代换得到∠ABC=∠ACB, 根据等腰三角形的判定定理即可证得AB=AC.
(3)过A点作AD⊥BC,有三线合一可知AD平分BC,点O在AD上,连结OB,则∠BOD=∠BAC,根据圆周角定理可知∠BOD=∠BAC, ∠BPC=∠BAC,由∠BOD=∠BPC可得 ![]() ,设OB=
,设OB=![]() ,根据勾股定理可算出OB、BD、OD、AD的长,再次利用勾股定理即可求得AP的值.
,根据勾股定理可算出OB、BD、OD、AD的长,再次利用勾股定理即可求得AP的值.
解:(1)∵点P是弧AB的中点,如图1,
∴AP=BP,
在△APC和△BPC中
 ,
,
∴△APC≌△BPC(SSS),
∴∠ACP=∠BCP,
在△ACE和△BCE中
 ,
,
∴△ACE≌△BCE(SAS),
∴∠AEC=∠BEC,
∵∠AEC+∠BEC=180°,
∴∠AEC=90°,
∴AB⊥PC;
(2)∵PA平分∠CPM,
∴∠MPA=∠APC,
∵∠APC+∠BPC+∠ACB=180°,∠MPA+∠APC+∠BPC=180°,
∴∠ACB=∠MPA=∠APC,
∵∠APC=∠ABC,
∴∠ABC=∠ACB,
∴AB=AC;
(3)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图2,

由(2)得出AB=AC,
∴AD平分BC,
∴点O在AD上,
连结OB,则∠BOD=∠BAC,
∵∠BPC=∠BAC,
∴![]() =
=![]() ,
,
设OB=25x,则BD=24x,
∴OD=![]() =7x,
=7x,
在![]() 中,AD=25x+7x=32x,BD=24x,
中,AD=25x+7x=32x,BD=24x,
∴AB=![]() =40x,
=40x,
∵AC=8,
∴AB=40x=8,
解得:x=0.2,
∴OB=5,BD=4.8,OD=1.4,AD=6.4,
∵点P是![]() 的中点,
的中点,
∴OP垂直平分AB,
∴AE=![]() AB=4,∠AEP=∠AEO=90°,
AB=4,∠AEP=∠AEO=90°,
在![]() 中,OE=
中,OE=![]() ,
,
∴PE=OP﹣OE=5﹣3=2,
在![]() 中,AP=
中,AP=![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:
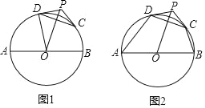
【题目】如图1,AB是⊙O的直径,P为⊙O外一点,C,D为⊙O上两点,连结OP,CD,PD=PC.已知AB=8.
(1)若OP=5,PD=3,求证:PD是⊙O的切线;
(2)若PD、PC是⊙O的切线;
①求证:OP⊥CD;
②连结AD,BC,如图2,若∠DAB=50°,∠CBA=70°,求弧CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,弧CD=弧CE.
(1)求证:OA=OB
(2)已知AB=4![]() ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,绘出了某一结果出现的频率的折线图,则符合这一结果的实验可能是
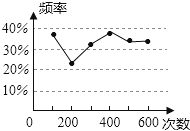
A. 掷一枚正六面体的骰子,出现1点的概率
B. 抛一枚硬币,出现正面的概率
C. 任意写一个整数,它能被2整除的概率
D. 从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,以线段
,以线段![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,过
,过![]() 、
、![]() 、
、![]() 三点作抛物线.
三点作抛物线.
(1)求抛物线的解析式;
(2)连结![]() ,
,![]() ,点
,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的角平分线
的角平分线![]() 交⊙
交⊙![]() 于点
于点![]() ,连结
,连结![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标;
的坐标;
(3)在(2)的条件下,抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
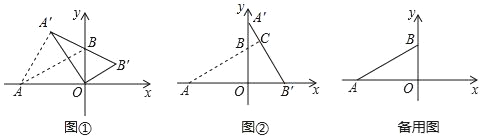
【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
(1)如图①,当点A′,B,B′共线时,求AA′的长.
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,∠AOB=60°,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资![]() (吨)与时间
(吨)与时间![]() (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
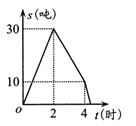
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为( )
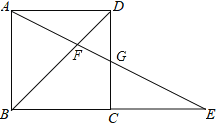
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com