
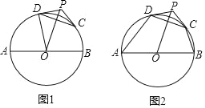
【题目】如图1,AB是⊙O的直径,P为⊙O外一点,C,D为⊙O上两点,连结OP,CD,PD=PC.已知AB=8.
(1)若OP=5,PD=3,求证:PD是⊙O的切线;
(2)若PD、PC是⊙O的切线;
①求证:OP⊥CD;
②连结AD,BC,如图2,若∠DAB=50°,∠CBA=70°,求弧CD的长.
【答案】(1)证明见解析;(2)①证明解析;②弧CD的长为![]() .
.
【解析】
1)利用勾股定理的逆定理证明∠DOP=90°即可.
(2)①如图1中,连接OC.由切线长定理可知PD=PC,因为OD=OC,所以OP垂直平分线段CD,由此即可解决问题.
②求出圆心角∠DOC的度数即可解决问题.
(1)证明:∵直径AB=8,
∴OD=4,
∵OP=5,PD=3,
∴OP2=PD2+OD2,
∴∠ODP=90°,
∴OD⊥DP,
∴PD是⊙O的切线.
(2)①证明:如图1中,连接OC.
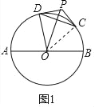
∵PD,PC是⊙O的切线,
∴PD=PC,
∵OD=OC,
∴OP垂直平分线段CD,
∴OP⊥CD.
②解:如图2中,连接OD,OC.
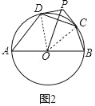
∵OA=OD,OB=OC,
∴∠A=∠ODA=50°,∠B=∠OCB=70°,
∴∠AOD=180°﹣100°=80°,∠BOC=180°﹣140°=40°,
∴∠DOC=180°﹣80°﹣40°=60°,
∴弧CD的长=![]() =
=![]() .
.
故答案为:(1)证明见解析;(2)①证明解析;②弧CD的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() ,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作
,点P为AB边上的一个动点,点E、F分别是CA,CB边的中点,过点P作![]() 于D,设
于D,设![]() ,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是
,图中某条线段的长为y,如果表示y与x的函数关系的大致图象如图2所示,那么这条线段可能是![]()
![]()
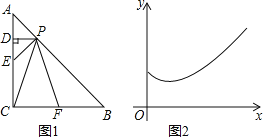
A. PDB. PEC. PCD. PF
查看答案和解析>>
科目:初中数学 来源: 题型:
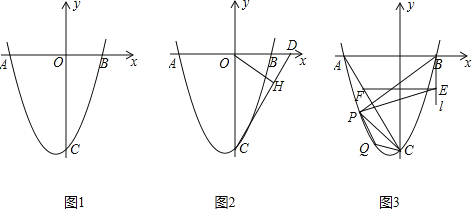
【题目】如图1,抛物线![]() 交x轴于点
交x轴于点![]() ,
,![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图2,D点坐标为
如图2,D点坐标为![]() ,连结
,连结![]() 若点H是线段DC上的一个动点,求
若点H是线段DC上的一个动点,求![]() 的最小值.
的最小值.
![]() 如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知
如图3,连结AC,过点B作x轴的垂线l,在第三象限中的抛物线上取点P,过点P作直线AC的垂线交直线l于点E,过点E作x轴的平行线交AC于点F,已知![]() .
.
![]() 求点P的坐标;
求点P的坐标;
![]() 在抛物线
在抛物线![]() 上是否存在一点Q,使得
上是否存在一点Q,使得![]() 成立?若存在,求出Q点坐标;若不存在,请说明理由.
成立?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某民营企业准备用14000元从外地购进A、B两种商品共600件,其中A种商品的成本价为20元,B种商品的成本价为30元.
(1)该民营企业从外地购得A、B两种商品各多少件?
(2)该民营企业计划租用甲、乙两种货车共6辆,一次性将A、B两种商品运往某城市,已知每辆甲种货车最多可装A种商品110件和B种商品20件;每辆乙种货车最多可装A种商品30件和B种商品90件,问安排甲、乙两种货车有几种方案?请你设计出具体的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点P是射线BA上的一个动点,以BP为半径的
,点P是射线BA上的一个动点,以BP为半径的![]() 交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点
交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点![]() ,连结
,连结![]() ,
,![]() ,设直线
,设直线![]() 与直线BC交于点F.
与直线BC交于点F.
![]() 当点P在线段BA上时,
当点P在线段BA上时,
![]() 求证:
求证:![]() ;
;
![]() 连结
连结![]() ,当
,当![]() 时,求
时,求![]() 的长;
的长;
![]() 连结AD,AF,当
连结AD,AF,当![]() 恰为等边三角形时,求此时四边形
恰为等边三角形时,求此时四边形![]() 的面积;
的面积;
![]() 当四边形
当四边形![]() 在
在![]() 内部时,请直接写出BP的取值范围.
内部时,请直接写出BP的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com