
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
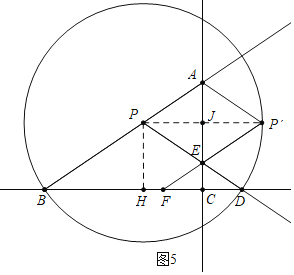
,![]() ,点P是射线BA上的一个动点,以BP为半径的
,点P是射线BA上的一个动点,以BP为半径的![]() 交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点
交射线BC于点D,直线PD交直线AC于点E,点P关于直线AC的对称点为点![]() ,连结
,连结![]() ,
,![]() ,设直线
,设直线![]() 与直线BC交于点F.
与直线BC交于点F.
![]() 当点P在线段BA上时,
当点P在线段BA上时,
![]() 求证:
求证:![]() ;
;
![]() 连结
连结![]() ,当
,当![]() 时,求
时,求![]() 的长;
的长;
![]() 连结AD,AF,当
连结AD,AF,当![]() 恰为等边三角形时,求此时四边形
恰为等边三角形时,求此时四边形![]() 的面积;
的面积;
![]() 当四边形
当四边形![]() 在
在![]() 内部时,请直接写出BP的取值范围.
内部时,请直接写出BP的取值范围.

【答案】![]() 证明见解析;②
证明见解析;②![]() .(2)①
.(2)①![]() .②
.②![]() .(3)
.(3)![]() .
.
【解析】
![]() 欲证明
欲证明![]() ,利用等角的余角相等证明
,利用等角的余角相等证明![]() 即可;
即可;![]() 如图2中,作
如图2中,作![]() 于H,连接
于H,连接![]() 交AC于点
交AC于点![]() 设
设![]() ,则
,则![]() 易知
易知![]() ,根据
,根据![]() ,可得
,可得![]() ,推出
,推出![]() ,由
,由![]() ,可得
,可得![]() ,由此即可解决问题;
,由此即可解决问题;
![]() 分两种情形分别求解即可:
分两种情形分别求解即可:![]() 如图3中,当点D在BC上时
如图3中,当点D在BC上时![]() 如图4中,当点D在BC的延长线上时,分别求解即可;
如图4中,当点D在BC的延长线上时,分别求解即可;
![]() 如图4中,当点
如图4中,当点![]() 在
在![]() 上时,设
上时,设![]() 则
则![]() ,构建方程求出m的值即可解决问题.
,构建方程求出m的值即可解决问题.
![]() 证明:如图1中,
证明:如图1中,
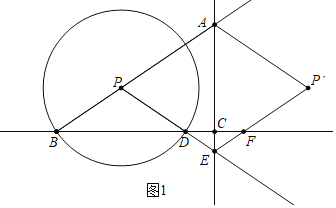
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 如图2中,作
如图2中,作![]() 于H,连接
于H,连接![]() 交AC于点
交AC于点![]() 设
设![]() ,则
,则![]() .
.
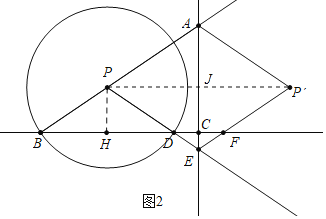
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 如图3中,当点D在BC上时,连接AD,AF,作
如图3中,当点D在BC上时,连接AD,AF,作![]() 于H,连接
于H,连接![]() 交AC于点J.
交AC于点J.
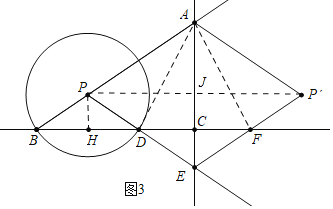
![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形PJCH是矩形,
四边形PJCH是矩形,
![]() ,
,
![]() ,
,
![]() .
.
![]() 如图4中,当点D在BC的延长线上时,连接AD,AF,当
如图4中,当点D在BC的延长线上时,连接AD,AF,当![]() 是等边三角形时,作
是等边三角形时,作![]() 于H,连接
于H,连接![]() 交AC于点J.
交AC于点J.
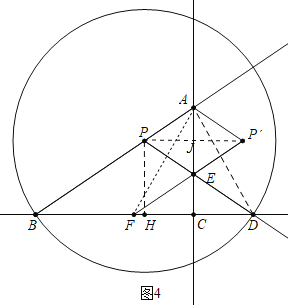
同法可得:![]() ,
,![]() ,
,
![]() .
.
![]() 如图4中,当点
如图4中,当点![]() 在
在![]() 上时,设
上时,设![]() 则
则![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
观察图象可知:当四边形![]() 在
在![]() 内部时,BP的取值范围为
内部时,BP的取值范围为![]() .
.


科目:初中数学 来源: 题型:
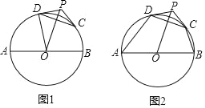
【题目】如图1,AB是⊙O的直径,P为⊙O外一点,C,D为⊙O上两点,连结OP,CD,PD=PC.已知AB=8.
(1)若OP=5,PD=3,求证:PD是⊙O的切线;
(2)若PD、PC是⊙O的切线;
①求证:OP⊥CD;
②连结AD,BC,如图2,若∠DAB=50°,∠CBA=70°,求弧CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
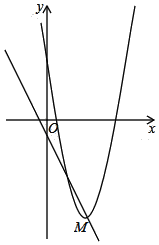
【题目】在平面直角坐标系中,抛物线![]() 的顶点M在直线L:
的顶点M在直线L:![]() 上.
上.
![]() 求直线L的函数表达式;
求直线L的函数表达式;
![]() 现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当
现将抛物线沿该直线L方向进行平移,平移后的抛物线的顶点为N,与x轴的右交点为C,连接NC,当![]() 时,求平移后的抛物线的解析式.
时,求平移后的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,弧CD=弧CE.
(1)求证:OA=OB
(2)已知AB=4![]() ,OA=4,求阴影部分的面积.
,OA=4,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,绘出了某一结果出现的频率的折线图,则符合这一结果的实验可能是
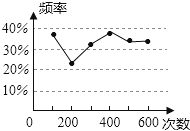
A. 掷一枚正六面体的骰子,出现1点的概率
B. 抛一枚硬币,出现正面的概率
C. 任意写一个整数,它能被2整除的概率
D. 从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资![]() (吨)与时间
(吨)与时间![]() (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
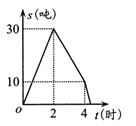
A. 4小时B. 4.3小时C. 4.4小时D. 5小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com