
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形.
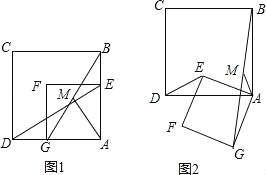
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
【答案】(1)AM=![]() DE,AM⊥DE,理由详见解析;(2)AM=
DE,AM⊥DE,理由详见解析;(2)AM=![]() DE,AM⊥DE,理由详见解析.
DE,AM⊥DE,理由详见解析.
【解析】
试题分析:(1)AM=![]() DE,AM⊥DE,理由是:先证明△DAE≌△BAG,得DE=BG,∠AED=∠AGB,再根据直角三角形斜边的中线的性质得AM=
DE,AM⊥DE,理由是:先证明△DAE≌△BAG,得DE=BG,∠AED=∠AGB,再根据直角三角形斜边的中线的性质得AM=![]() BG,AM=BM,则AM=
BG,AM=BM,则AM=![]() DE,由角的关系得∠MAB+∠AED=90°,所以∠AOE=90°,即AM⊥DE;(2)AM=
DE,由角的关系得∠MAB+∠AED=90°,所以∠AOE=90°,即AM⊥DE;(2)AM=![]() DE,AM⊥DE,理由是:作辅助线构建全等三角形,证明△MNG≌△MAB和△AGN≌△EAD可以得出结论.
DE,AM⊥DE,理由是:作辅助线构建全等三角形,证明△MNG≌△MAB和△AGN≌△EAD可以得出结论.
试题解析:(1)AM=![]() DE,AM⊥DE,理由是:
DE,AM⊥DE,理由是:
如图1,设AM交DE于点O,
∵四边形ABCD和四边形AEFG都是正方形,
∴AG=AE,AD=AB,
∵∠DAE=∠BAG,
∴△DAE≌△BAG,
∴DE=BG,∠AED=∠AGB,
在Rt△ABG中,
∵M为线段BG的中点,
∴AM=![]() BG,AM=BM,
BG,AM=BM,
∴AM=![]() DE,
DE,
∵AM=BM,
∴∠MBA=∠MAB,
∵∠AGB+∠MBA=90°,
∴∠MAB+∠AED=90°,
∴∠AOE=90°,即AM⊥DE;
(2)AM=![]() DE,AM⊥DE,理由是:
DE,AM⊥DE,理由是:
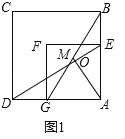
如图2,延长AM到N,使MN=AM,连接NG,
∵MN=AM,MG=BM,∠NMG=∠BMA,
∴△MNG≌△MAB,
∴NG=AB,∠N=∠BAN,
由(1)得:AB=AD,
∴NG=AD,
∵∠BAN+∠DAN=90°,
∴∠N+∠DAN=90°,
∴NG⊥AD,
∴∠AGN+∠DAG=90°,
∵∠DAG+∠DAE=∠EAG=90°,
∴∠AGN=∠DAE,
∵NG=AD,AG=AE,
∴△AGN≌△EAD,
∴AN=DE,∠N=∠ADE,
∵∠N+∠DAN=90°,
∴∠ADE+∠DAN=90°,
∴AM⊥DE.



科目:初中数学 来源: 题型:
【题目】有两名流感病人,如果每轮传播中平均一个病人传染的人数相同,为了使两轮传播后,流感病人总数不超过288人,则每轮传播中平均一个病人传染的人数不能超过人.
查看答案和解析>>
科目:初中数学 来源: 题型:
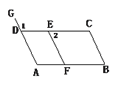
【题目】如图,点E在CD上,点F在BA上,G是AD延长线上一点.
(1 )若∠A=∠1,则可判断_______∥_______,因为________.
(2 )若∠1=∠_________,则可判断AG∥BC,因为_________.
(3 )若∠2+∠______=180°,则可判断CD∥AB,因为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
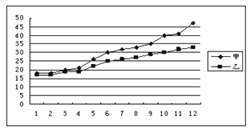
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A. 甲运动员得分的极差大于乙运动员得分的极差
B. 甲运动员得分的中位数大于乙运动员得分的中位数
C. 甲运动员得分的平均数大于乙运动员得分的平均数
D. 甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(﹣1,0),与y轴的交点坐标为(0,3).
(1)求出b、c的值,并写出此二次函数的解析式;
(2)根据图象,直接写出函数值y为正数时,自变量x的取值范围;
(3)当2≤x≤4时,求y的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有甲、乙两种出租车,他们的服务质量相同.甲的计价方式为:当行驶路程不超过3千米时收费10元,每超过1千米则另外收费1.2元(不足1千米按1千米收费);乙的计价方式为:当行驶路程不超过3千米时收费8元,每超过1千米则另外收费1.8元(不足1千米按1千米收费).某人到该市出差,需要乘坐的路程为x千米.
(1)当x=5时,请分别求出乘坐甲、乙两种出租车的费用;
(2)用代数式表示此人分别乘坐甲、乙出租车各所需要的费用;
(3)假设此人乘坐的路程为13千米多一点,请问他乘坐哪种车较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点C沿着某条路径运动,以C为旋转中心,将点A(0,4)逆时针旋转60度,到B(m,1).若![]() ,则点C的运动路径长是_________________。
,则点C的运动路径长是_________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com