
【题目】已知函数y=(2m+3)x+m-1.
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴上的的交点位于原点上方,求m的取值范围;
(3)若函数图象平行于直线y=x+1,求m的值;
(4)若该函数的值y随自变量x的增大而减小,求m的取值范围.
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为( )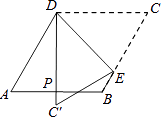
A.78°
B.75°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索. 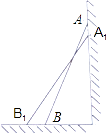
【思考题】如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
(1)请你将小明对“思考题”的解答补充完整: 解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1= ![]() ﹣0.4=2
﹣0.4=2
而A1B1=2.5,在Rt△A1B1C中,由 ![]() 得方程 ,
得方程 ,
解方程得x1= , x2= ,
∴点B将向外移动米.
(2)解完“思考题”后,小聪提出了如下两个问题: 【问题一】在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
【问题二】在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
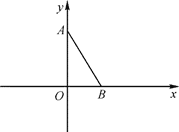
【题目】如图,平面直角坐标系 xOy 中,已知点 A(0,3),点 B(![]() ,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”
,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”
(1)在点 C1 (-2, ![]() ),点 C2 (0,-2),点 C3 (
),点 C2 (0,-2),点 C3 (![]() ,
, ![]() )中,线段 AB 的“等长点”是点______________;
)中,线段 AB 的“等长点”是点______________;
(2)若点 D( m , n )是线段 AB 的“等长点”,且∠DAB=60,求 m 和 n 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )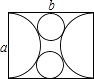
A.b= ![]() a
a
B.b= ![]() a
a
C.b= ![]()
D.b= ![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )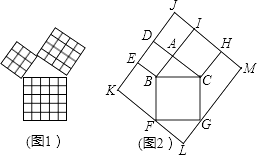
A.90
B.100
C.110
D.121
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4).
(1)求反比例函数的解析式和点B的坐标;
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠A=90°,∠B=120°,AD= ![]() ,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°.
,AB=6.在底边AB上取点E,在射线DC上取点F,使得∠DEF=120°. 
(1)当点E是AB的中点时,线段DF的长度是;
(2)若射线EF经过点C,则AE的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小三角形,若 ![]() =
= ![]() ,则△ABC的边长是 .
,则△ABC的边长是 . 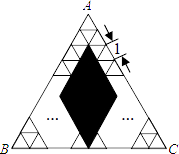
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com