
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.

(1)判断DE与⊙O的位置关系并说明理由;
(2)若AC=16,tanA=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)DE与⊙O相切.理由见解析;(2)5.
【解析】试题分析:(1)连接DO,BD,如图,由于∠BDE=∠A,∠A=∠ADO,则∠ADO=∠EDB,再根据圆周角定理得∠ADB=90°,所以∠ADO+∠ODB=90°,于是得到∠ODB+∠EDB=90°,然后根据切线的判定定理可判断DE为⊙O的切线;
(2)利用等角的余角相等得∠ABD=∠EBD,加上BD⊥AC,根据等腰三角形的判定方法得△ABC为等腰三角形,所以AD=CD=![]() AC=8,然后在Rt△ABD中利用正切定义可计算出BD=6,再根据勾股定理计算出AB,从而得到⊙O的半径.
AC=8,然后在Rt△ABD中利用正切定义可计算出BD=6,再根据勾股定理计算出AB,从而得到⊙O的半径.
试题解析:(1)DE与⊙O相切.理由如下:
连接DO,BD,如图,

∵∠BDE=∠A,∠A=∠ADO,
∴∠ADO=∠EDB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ODB+∠EDB=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∵∠BDE=∠A,
∴∠ABD=∠EBD,
而BD⊥AC,
∴△ABC为等腰三角形,
∴AD=CD=![]() AC=8,
AC=8,
在Rt△ABD中,
∵tanA=![]() ,
,
∴BD=![]() ×8=6,
×8=6,
∴AB=![]() =10,
=10,
∴⊙O的半径为5.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4![]() ,∠BAC=45°.
,∠BAC=45°.
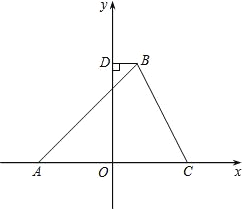
(1)求点A,C的坐标;
(2)反比例函数y=![]() 的图象经过点B,求k的值;
的图象经过点B,求k的值;
(3)在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P,O,A为顶点的三角形相似?若存在,请写出满足条件的点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种面粉的质量标识为“26±0.25千克”,则下列面粉中合格的是:( )
A. 26.30千克 B. 25.70千克 C. 26.51千克 D. 25.80千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+xn)的结果是( )
A.1﹣xn+1
B.1+xn+1
C.1﹣xn
D.1+xn
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com