
分析 此题要分两种情况进行讨论:(1)当等腰三角形的顶角是钝角时,腰上的高在三角形的外部,先在Rt△ACO中由勾股定理求出AO=4,于是OB=AB+AO=9,然后在Rt△BCO中利用勾股定理即可求出BC即可;
(2)当等腰三角形的顶角是锐角时,腰上的高在三角形的内部,在Rt△ACO中由勾股定理求出AD=4,于是DB=AB-AD=1,然后在Rt△BCD中利用勾股定理求出BC即可.
解答 解:分两种情况: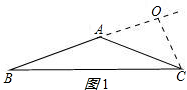
(1)顶角是钝角时,如图1所示:
在Rt△ACO中,由勾股定理,得AO2=AC2-OC2=52-32=16,
∴AO=4,
OB=AB+AO=5+4=9,
在Rt△BCO中,由勾股定理,得BC2=OB2+OC2=92+32=90,
∴BC=$\sqrt{90}$=3$\sqrt{10}$;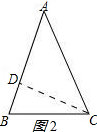
(2)顶角是锐角时,如图2所示:
在Rt△ACD中,由勾股定理,得AD2=AC2-DC2=52-32=16,
∴AD=4,
DB=AB-AD=5-4=1.
在Rt△BCD中,由勾股定理,得BC2=DB2+DC2=12+32=10,
∴BC=$\sqrt{10}$;
综上可知,这个等腰三角形的底的长度为3$\sqrt{10}$或$\sqrt{10}$.
故答案为:3$\sqrt{10}$或$\sqrt{10}$.
点评 本题考查了勾股定理及等腰三角形的性质,难度适中,分情况讨论是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
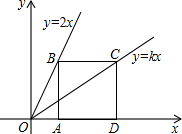 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.
如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型号客车 | B型号客车 | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 280 |
| 车辆数(辆) | a | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
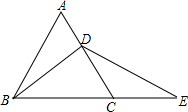 如图所示,△ABC为等边三角形,BD为中线,延长BC至E,使 DE=BD.
如图所示,△ABC为等边三角形,BD为中线,延长BC至E,使 DE=BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$.
如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com