Question

【题目】已知，在平面直角从标系中，A点坐标为（0，4），B点坐标为（2，0），C（m，6）为反比例函数 图象上一点．将△AOB绕B点旋转至△A′O′B处．

（1）求m的值；
（2）若O′落在OC上，连接AA′交OC与D点．①求证：四边形ACA′O′为平行四边形； ②求CD的长度；
（3）直接写出当AO′最短和最长时A′点的坐标．

Answer 1

【答案】
（1）

解：∵C（m，6）为反比例函数 图象上一点，

∴m= = ；

（2）

如图1．

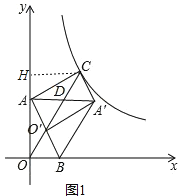
∵点C的坐标为（ ，6），∴CH= ，OH=6，∴tan∠COH= ，AC=

∴∠COH=30°，OA=AC，

∴∠BOO′=60°，∠ACO=∠AOC=30°．

∵BO′=BO，

∴∠BO′O=∠BOO′=60°．

∵∠A′O′B=∠AOB=90°，

∴∠CO′A′=30°，

∴∠ACO=∠CO′A′，

∴AC∥O′A′．

又∵O′A′=OA=AC，

∴四边形ACA′O′为平行四边形；

②∵BO′=BO，∠BOO′=60°，

∴△BOB′是等边三角形，

∴OO′=OB=2．

∵∠CHO=90°，CH= ，OH=6，∴OC= ，∴CO′=OC﹣OO′= ﹣2．

∵四边形ACA′O′为平行四边形，

∴CD=O′D= CO′= ﹣1；

（3）

解：当AO′最短时A′点的坐标（2+ ， ），当AO′最长时A′点的坐标（2﹣ ，﹣ ）．

提示：①当点O′在线段AB上时，AO′最短，

过点O′作O′N⊥x轴于N，过点A′作A′M⊥O′N于M，如图2．

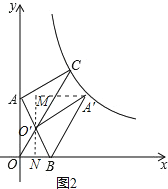
∵O′N∥OA，

∴△BNO′∽△BOA，

∴ ，

∴ ，

∴BN= ，O′N= ．

∵∠A′MO′=∠A′O′B=∠O′NB=90°，

∴∠MA′O′=∠NO′B，

∴△A′MO′∽△O′NB，

∴ ，

∴A′M= ，O′M= ，

∴A′（2﹣ + ， + ）即（2+ ， ）；

②当点O′在线段AB延长线上时，AO′最长，

过点O′作O′N⊥x轴于N，过点A′作A′M⊥O′N于M，如图3．’

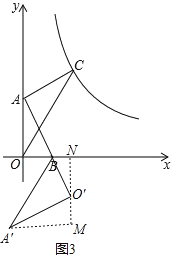
同理可得：A′（2﹣ ，﹣ ）

【解析】（1）只需把点C的坐标代入反比例函数的解析式，就可解决问题；（2）①过点C作CH⊥y轴与H，如图1，易证AC=OA=O′A′，要证四边形ACA′O′为平行四边形，只需证AC∥O′A′，只需证∠ACO=∠A′O′C即可；②由平行四边形ACA′O′可得CD= CO′，要求CD，只需求CO′，只需求出OC及OO′即可；（3）根据两点之间线段最短可知：当点O′在线段AB上时AO′最短（如图2），当点O′在线段AB的延长线上时AO′最长（如图3）；过点O′作O′N⊥x轴于N，过点A′作A′M⊥O′N于M，易证△BNO′∽△BOA，△A′MO′∽△O′NB，然后只需运用相似三角形的性质即可解决问题．