
【题目】计算:| ![]() -
- ![]() |+(
|+( ![]() -1)0+2sin45°﹣2cos30°+(
-1)0+2sin45°﹣2cos30°+( ![]() )﹣1 .
)﹣1 .
【答案】解:| ![]() -
- ![]() |+(
|+( ![]() -1)0+2sin45°﹣2cos30°+(
-1)0+2sin45°﹣2cos30°+( ![]() )﹣1
)﹣1
= ![]() ﹣
﹣ ![]() +1+2×
+1+2× ![]() ﹣2×
﹣2× ![]() +2015
+2015
= ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +2015
+2015
=2015.
【解析】直接利用零指数幂的性质以及绝对值的性质、负整数指数幂的性质、特殊角的三角函数值分别化简求出答案.此题主要考查了实数运算,根据相关运算法则正确化简是解题关键.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数),以及对整数指数幂的运算性质的理解,了解aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+5经过点M(1,3)和N(3,5)
(1)试判断该抛物线与x轴交点的情况;
(2)平移这条抛物线,使平移后的抛物线经过点A(﹣2,0),且与y轴交于点B,同时满足以A、O、B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】望江中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)m=%,n=%,这次共抽查了名学生进行调查统计;
(2)请补全上面的条形图;
(3)如果该校共有1200名学生,请你估计该校C类学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c(a≠0)有一个根为﹣ ![]()
其中正确的结论个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.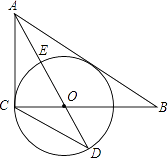
(1)求证:AB是⊙O的切线.
(2)已知AO角⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,求
,求 ![]() 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
说明:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点
纸片利用率= ![]() ×100%
×100%
发现:

(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
说明:方案三中的每条边均过其中两个正方形的顶点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角从标系中,A点坐标为(0,4),B点坐标为(2,0),C(m,6)为反比例函数 ![]() 图象上一点.将△AOB绕B点旋转至△A′O′B处.
图象上一点.将△AOB绕B点旋转至△A′O′B处.
(1)求m的值;
(2)若O′落在OC上,连接AA′交OC与D点.①求证:四边形ACA′O′为平行四边形; ②求CD的长度;
(3)直接写出当AO′最短和最长时A′点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com