Question

5．有一块三角形绿地，三角形绿地的两个内角分别为30°和45°，量得绿地的一条边长为30m，求这块绿地的面积（画出图形，直接写出答案，并画出体现解法的辅助线）．

Answer 1

分析 分三种情形讨论即可：①当BC=30时，$\sqrt{3}$a+a=30，②当AB=30时，2a=30，③当AC=30时，$\sqrt{2}$a=30，解方程即可．

解答 解：如图△ABC中，∠B=30°，∠C=45°，作AM⊥BC于M．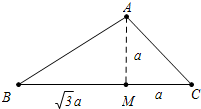
在RT△AMC中，∵∠AMC=90°，∠C=45°，
∴∠MAC=∠=45°，
∴AM=MC，AC=$\sqrt{2}$AM，
在RT△ABM中，∵∠B=30°，∠AMB=90°，
∴AB=2AM，BM=$\sqrt{3}$AM，
设AM=MC=a，则AB=2a，BM=$\sqrt{3}$a，AC=$\sqrt{2}$a，
①当BC=30时，$\sqrt{3}$a+a=30，a=15（$\sqrt{3}$-1），S_△ABC=$\frac{1}{2}$×$30×15（\sqrt{3}-1）$=225$\sqrt{3}$-225．
②当AB=30时，2a=30，a=15，S_△ABC=$\frac{1}{2}$•（15$\sqrt{3}$+15）•15=$\frac{225\sqrt{3}+225}{2}$．
③当AC=30时，$\sqrt{2}$a=30，a=15$\sqrt{2}$，S_△ABC=$\frac{1}{2}$•（15$\sqrt{6}$+15$\sqrt{2}$）•15$\sqrt{2}$=225$\sqrt{3}$+225．

点评 本题考查勾股定理、特殊三角形的边角关系，解题的关键是记住特殊三角形的边之间的关系，属于中考常考题型．