
分析 根据(ab)n=anbn,可得(3+$\sqrt{2}$)2×(3-$\sqrt{2}$)2=[(3+$\sqrt{2}$)×(3-$\sqrt{2}$)]2,据此求出算式(3+$\sqrt{2}$)2×(3-$\sqrt{2}$)2的值是多少即可.
解答 解:(3+$\sqrt{2}$)2×(3-$\sqrt{2}$)2
=[(3+$\sqrt{2}$)×(3-$\sqrt{2}$)]2
=[${3}^{2}{-(\sqrt{2})}^{2}$]2
=72
=49.
故答案为:49.
点评 (1)此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.
(2)此题还考查了积的乘方,要熟练掌握,解答此题的关键是要明确:(ab)n=anbn(n是正整数).


科目:初中数学 来源: 题型:选择题
| 物体的质量(kg) | 0 | 1 | 2 | 4 | 5 | … |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 14 | 14.5 | … |
| A. | 15cm | B. | 15.6cm | C. | 15.8cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1-3x}{-x-2}$=$\frac{3x-1}{x+2}$ | B. | $\frac{-2{x}^{3}y}{4{x}^{2}{y}^{2}}$=-$\frac{x}{2y}$ | ||
| C. | (x2-xy)÷$\frac{x-y}{x}$=(x-y)2 | D. | $\frac{4}{x-2}$+$\frac{x+2}{2-x}$=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
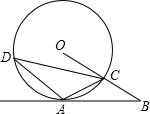 已知,如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=$\frac{1}{2}$OB.
已知,如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=$\frac{1}{2}$OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
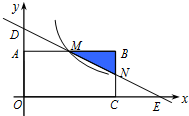 如图,在直角坐标系中,长方形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图,在直角坐标系中,长方形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
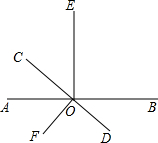 如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,
如图,直线AB与CD相交于D,OE⊥AB,OF⊥CD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com