练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．若x=$\sqrt{29}$-3，则$\sqrt{{x}^{2}+6x+5}$的值为5．

    分析 先把x=$\sqrt{29}$-3变形得到x+3=$\sqrt{29}$，由x2+6x+5=（x+3）2-4，然后整体代入进行计算．

    解答 解：∵x=$\sqrt{29}$-3，
    ∴x+3=$\sqrt{29}$，
    ∴$\sqrt{{x}^{2}+6x+5}$=$\sqrt{（x+3）^{2}-4}$=5．
    故答案为：5．

    点评 本题考查了二次根式的化简求值，利用完全平方公式变形所求的代数式，再运用整体代入的方法求代数式的值

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．若$\sqrt{5}$的小数部分为a，$\sqrt{13}$的小数部分为b，求a+b-$\sqrt{5}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，点A在双曲线y=$\frac{6}{x}$上，B为x轴正半轴上一点，连结OA、AB且AO=AB，则△AOB的面积是6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知x1，x2为方程x2+3x+1=0两个实根，则x12-3x2+x1x2=9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．已知a＜0，那么$\sqrt{（a-1{）^2}}+\sqrt{a^2}$可化简为（　　）
    A．2a-1B．1-2aC．-1D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

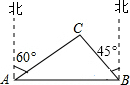    7．我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路（记作AB）．已知C点周围700米范围内有一电力设施区域．在A处测得C在A的北偏东60°方向上，在B处测得C在B的北偏西45°方向上．（$\sqrt{3}$≈1.7，$\sqrt{2}$≈1.4）
    （1）道路AB是否穿过电力设施区域？为什么？
    （2）在施工500米后，为了尽量减少施工对城市交通所造成的影响，加快了施工进度，实际工作效率变成了原计划工作效率的1.5倍，结果提前5天完成了修路任务，则原计划每天修路多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．已知如图：点A、B、C、D在⊙O上，AB为直径，∠ABC=72°，则∠D为（　　）
    A．18°B．30°C．36°D．72°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．在$\frac{1}{x}$，$\frac{1}{2}$，$\frac{1}{2}（{x^2}+1）$，$\frac{3xy}{π}$，$\frac{3}{x+y}$中，分式的个数为（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．把cos12°、sin21°、cos67°、sin69°排列大小正确的是（　　）
    A．cos12°＜sin21°＜cos67°＜sin69°B．sin21°＜cos12°＜cos67°＜sin69°
    C．sin21°＜cos67°＜sin69°＜cos12°D．cos67°＜cos12°＜sin21°＜sin69°

    查看答案和解析>>

    同步练习册答案