
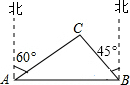
 我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)分析 (1)首先过点C作CD⊥AB于点D,设CD=x米,然后利用三角函数,即可表示出AD与BD的长,继而可得方程$\sqrt{3}$x+x=2000,解此方程即可求得CD的长,与700米比较,即可得道路AB不穿过电力设施区域;
(2)首先设原计划每天修路y米,根据题意即可得分式方程:$\frac{2000}{y}$-5=$\frac{2000-500}{1.5y}$+$\frac{500}{y}$,解此分式方程即可求得答案
解答 解:(1)道路AB不穿过电力设施区域.
过点C作CD⊥AB于点D,
设CD=x米,
由题意得:∠CAD=90°-60°=30°,∠CBD=90°-45°=45°,
在Rt△ACD中,AD=$\frac{CD}{tan30°}$=$\sqrt{3}$x(米),
在Rt△BCD中,BD=CD=x(米),
∵AB=2000米,
∴$\sqrt{3}$x+x=2000,
解得:x=1000$\sqrt{3}$-1000≈732,
∵732米>700米,
∴道路AB不穿过电力设施区域;
(2)设原计划每天修路y米,
依题意得:$\frac{2000}{y}$-5=$\frac{2000-500}{1.5y}$+$\frac{500}{y}$,
解得:y=100,
经检验,y=100是原分式方程的解.
答:原计划每天修路100米.
点评 此题考查了方向角问题与分式方程的应用.此题难度适中,注意构造直角三角形并利用解直角三角形的知识求解是解此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 家庭人口数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 家庭数 | 20 | 29 | 48 | 50 | 46 | 36 | 19 | 8 | 4 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 150,100 | B. | 125,75 | C. | 120,70 | D. | 100,150 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 晚上,一个身高1.6米的人站在路灯下,发现自己的影子刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度?
晚上,一个身高1.6米的人站在路灯下,发现自己的影子刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com