
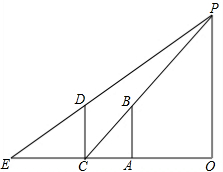
 晚上,一个身高1.6米的人站在路灯下,发现自己的影子刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度?
晚上,一个身高1.6米的人站在路灯下,发现自己的影子刚好是4块地砖的长(地砖是边长为0.5米的正方形),当他沿着影子的方向走了4块地砖时,发现自己的影子刚好是5块地砖的长,根据他的发现,你能不能计算路灯的高度? 分析 如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,先证明△CAB∽△COP,利用相似比得到$\frac{1.6}{OP}$=$\frac{2}{2+AO}$①,再证明△ECD∽△EOP得到$\frac{1.6}{OP}$=$\frac{2.5}{2.5+2+AO}$②,然后解关于OP和AO的方程组求出OP即可.
解答  解:如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,
解:如图,AC=4×0.5m=2m,CE=5×0.5m=2.5m,AB=CD=1.6m,
∵AB∥OP,
∴△CAB∽△COP,
∴$\frac{AB}{OP}$=$\frac{CA}{CO}$,即$\frac{1.6}{OP}$=$\frac{2}{2+AO}$①,
∵CD∥OP,
∴△ECD∽△EOP,
∴$\frac{CD}{OP}$=$\frac{EC}{EO}$,即$\frac{1.6}{OP}$=$\frac{2.5}{2.5+2+AO}$②,
由①②得$\frac{2}{2+AO}$=$\frac{2.5}{2.5+2+AO}$,解得AO=8,
∴$\frac{1.6}{OP}$=$\frac{2}{2+8}$,解得OP=8.
答:路灯的高度为8m.
点评 本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
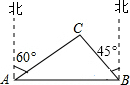 我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
我市某旗在棚户区改造工程中需要修建一段东西方向全长2000米的道路(记作AB).已知C点周围700米范围内有一电力设施区域.在A处测得C在A的北偏东60°方向上,在B处测得C在B的北偏西45°方向上.($\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | cos12°<sin21°<cos67°<sin69° | B. | sin21°<cos12°<cos67°<sin69° | ||
| C. | sin21°<cos67°<sin69°<cos12° | D. | cos67°<cos12°<sin21°<sin69° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x-1 | B. | y=-$\frac{1}{x}$ | C. | y=2x2-3x+1 | D. | y=$\frac{1}{{{x^2}-2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的弧所对的弦相等 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| C. | 经过圆心的角是圆心角 | |
| D. | 经过三个点一定可以做一个圆 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com